设等差数列满足，。

（Ⅰ）求的通项公式；

（Ⅱ）求的前项和及使得最大的序号的值。

4男3女站成一排，求满足下列条件的排法共有多少种？

任何两名女生都不相邻，有多少种排法？

男甲不在首位，男乙不在末位，有多少种排法？

男生甲、乙、丙顺序一定，有多少种排法？

男甲在男乙的左边不一定相邻有多少种不同的排法？

设x、y、zÎR₊，若xy + yz + zx = 1，则x + y + z的取值范围是__________

已知双曲线的实轴的长度比虚轴的长度大2，焦距为10，则双曲线的方程为

A.       B.       C.       D.

已知向量=（0,2,1），=（-1,1,-2）,则与的夹角的大小为               ．

已知复数满足，则复数在复平面内的对应点所在象限是（    ）

A．第一象限         B．第二象限       C．第三象限       D．第四象限

 已知函数

（1）若为曲线的一条切线，求a的值；

（2）已知，若存在唯一的整数，使得，求a的取值范围.

已知函数,

（1）.当时,求函数在区间上的最值

（2）.若,是函数的两个极值点,且,求证:

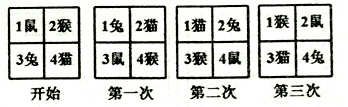
四个小动物换座位，开始是鼠、猴、兔、猫分别坐1、2、3、4号位上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，…这样交替进行下去，那么第202次互换座位后，小兔坐在第______号座位上．

曲线y=1+（﹣2≤x≤2）与直线y=k（x﹣2）+4有两个交点时，实数k的取值范围是（　　）

A．[，+∞）     B．（，]        C．（0，）       D．（，]

从字母中选出4个数字排成一列，其中一定要选出和，

并且必须相邻（在的前面），共 排列方法（    ）种.

A.      B．     C．     D．

 已知函数f(x)＝求f(x)在区间[－1,3π]上的定积分

.一质点在直线上从时刻t=0(s)开始以速度运动。求：（1）在t=4s的位置（2）在t=4s质点运动的路程

若函数f（x）=x•e^x+f′（﹣1）•x²，则f′（﹣1）=　   　．

过点Q(2,1)作抛物线y²＝8x的弦AB，恰被Q所平分．

(1)求AB所在直线方程；

(2)求|AB|的长．

已知集合（       ）

A.     B.     C.     D.

命题：“，”的否定为（  ）

    A.    B.

C.     D.，

在三次独立重复试验中，事件A在每次试验中发生的概率相同，若事件A至少发生一次的概率为，则事件A恰好发生一次的概率为(　　)

A.    B.    C.  D.

下图给出的计算的值的一个程序框图，其中判断框内应填入的条件是（ ）

A．         B．       C.          D．

 已知△ABC的周长为20，且顶点B （0，﹣4），C （0，4），则顶点A的轨迹方程是（    ）

A．（x≠0）                       B．（x≠0）

C．（x≠0）                        D．（x≠0）