жһҒйҷҗеҸҠе…¶иҝҗз®— зҹҘиҜҶзӮ№йўҳеә“
е·ІзҹҘеҮҪж•° пјҢ еҲҷ
пјҢ еҲҷ пјҲ пјү
пјҲ пјү
 пјҢ еҲҷ
пјҢ еҲҷ пјҲ пјү
пјҲ пјү
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
и®ҫf пјҲxпјүдёәеҸҜеҜјеҮҪж•°пјҢдё”ж»Ўи¶і  =п№Ј1пјҢеҲҷжӣІзәҝy=fпјҲxпјүеңЁзӮ№пјҲ1пјҢfпјҲ1пјүпјүеӨ„зҡ„еҲҮзәҝзҡ„ж–ңзҺҮжҳҜпјҲВ В пјү
=п№Ј1пјҢеҲҷжӣІзәҝy=fпјҲxпјүеңЁзӮ№пјҲ1пјҢfпјҲ1пјүпјүеӨ„зҡ„еҲҮзәҝзҡ„ж–ңзҺҮжҳҜпјҲВ В пјү
 =п№Ј1пјҢеҲҷжӣІзәҝy=fпјҲxпјүеңЁзӮ№пјҲ1пјҢfпјҲ1пјүпјүеӨ„зҡ„еҲҮзәҝзҡ„ж–ңзҺҮжҳҜпјҲВ В пјү
=п№Ј1пјҢеҲҷжӣІзәҝy=fпјҲxпјүеңЁзӮ№пјҲ1пјҢfпјҲ1пјүпјүеӨ„зҡ„еҲҮзәҝзҡ„ж–ңзҺҮжҳҜпјҲВ В пјү
A . 2
B . п№Ј1
C .  D . п№Ј2
D . п№Ј2
 D . п№Ј2
D . п№Ј2
 зҡ„еҖјдёәпјҺ
зҡ„еҖјдёәпјҺ
еңЁж•°еҲ—{an}дёӯпјҢan=пјҲп№Ј  пјүn пјҢ nвҲҲN* пјҢ еҲҷ
пјүn пјҢ nвҲҲN* пјҢ еҲҷ  anпјҲВ В пјү
anпјҲВ В пјү
 пјүn пјҢ nвҲҲN* пјҢ еҲҷ
пјүn пјҢ nвҲҲN* пјҢ еҲҷ  anпјҲВ В пјү
anпјҲВ В пјү
A . зӯүдәҺ  B . зӯүдәҺ0
C . зӯүдәҺ
B . зӯүдәҺ0
C . зӯүдәҺ  D . дёҚеӯҳеңЁ
D . дёҚеӯҳеңЁ
 B . зӯүдәҺ0
C . зӯүдәҺ
B . зӯүдәҺ0
C . зӯүдәҺ  D . дёҚеӯҳеңЁ
D . дёҚеӯҳеңЁ
иӢҘ  пјҢеҲҷ
пјҢеҲҷ  пјҲ пјү
пјҲ пјү
 пјҢеҲҷ
пјҢеҲҷ  пјҲ пјү
пјҲ пјү
A . -3
B . -12
C . -9
D . -6
и®Ўз®—пјҡ 

иӢҘеҮҪж•°  зҡ„еӨ§иҮҙеӣҫеғҸеҰӮеӣҫжүҖзӨәпјҢеҲҷ
зҡ„еӨ§иҮҙеӣҫеғҸеҰӮеӣҫжүҖзӨәпјҢеҲҷ  зҡ„и§ЈжһҗејҸеҸҜд»ҘдёәпјҲ пјү
зҡ„и§ЈжһҗејҸеҸҜд»ҘдёәпјҲ пјү
 зҡ„еӨ§иҮҙеӣҫеғҸеҰӮеӣҫжүҖзӨәпјҢеҲҷ
зҡ„еӨ§иҮҙеӣҫеғҸеҰӮеӣҫжүҖзӨәпјҢеҲҷ  зҡ„и§ЈжһҗејҸеҸҜд»ҘдёәпјҲ пјү
зҡ„и§ЈжһҗејҸеҸҜд»ҘдёәпјҲ пјү 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
иӢҘжӣІзәҝ  еӯҳеңЁдёӨжқЎеһӮзӣҙдәҺyиҪҙзҡ„еҲҮзәҝпјҢеҲҷmзҡ„еҸ–еҖјиҢғеӣҙдёә.
еӯҳеңЁдёӨжқЎеһӮзӣҙдәҺyиҪҙзҡ„еҲҮзәҝпјҢеҲҷmзҡ„еҸ–еҖјиҢғеӣҙдёә.
 еӯҳеңЁдёӨжқЎеһӮзӣҙдәҺyиҪҙзҡ„еҲҮзәҝпјҢеҲҷmзҡ„еҸ–еҖјиҢғеӣҙдёә.
еӯҳеңЁдёӨжқЎеһӮзӣҙдәҺyиҪҙзҡ„еҲҮзәҝпјҢеҲҷmзҡ„еҸ–еҖјиҢғеӣҙдёә.
е·ІзҹҘеҮҪж•°  пјҢеҲҷ
пјҢеҲҷ  зҡ„еҖјдёәпјҲ пјү
зҡ„еҖјдёәпјҲ пјү
 пјҢеҲҷ
пјҢеҲҷ  зҡ„еҖјдёәпјҲ пјү
зҡ„еҖјдёәпјҲ пјү
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
е·ІзҹҘеҮҪж•°  .
.
 .
.
-
пјҲ1пјү жұӮиҜҒпјҡеҪ“
 ж—¶пјҢ
ж—¶пјҢ  пјӣ
пјӣ
-
пјҲ2пјү и®°
 пјҢиӢҘ
пјҢиӢҘ  жңүе”ҜдёҖйӣ¶зӮ№пјҢжұӮе®һж•°aзҡ„еҸ–еҖјиҢғеӣҙ.
жңүе”ҜдёҖйӣ¶зӮ№пјҢжұӮе®һж•°aзҡ„еҸ–еҖјиҢғеӣҙ.
е·ІзҹҘж•°еҲ—  ж»Ўи¶іпјҡ
ж»Ўи¶іпјҡ  пјҢдё”
пјҢдё”  дёәзӯүе·®ж•°еҲ—пјҢж•°еҲ—
дёәзӯүе·®ж•°еҲ—пјҢж•°еҲ—  зҡ„еүҚnйЎ№е’Ңдёә
зҡ„еүҚnйЎ№е’Ңдёә  .
.
 ж»Ўи¶іпјҡ
ж»Ўи¶іпјҡ  пјҢдё”
пјҢдё”  дёәзӯүе·®ж•°еҲ—пјҢж•°еҲ—
дёәзӯүе·®ж•°еҲ—пјҢж•°еҲ—  зҡ„еүҚnйЎ№е’Ңдёә
зҡ„еүҚnйЎ№е’Ңдёә  .
.
-
пјҲ1пјү жұӮ
 зҡ„йҖҡйЎ№е…¬ејҸпјӣ
зҡ„йҖҡйЎ№е…¬ејҸпјӣ
-
пјҲ2пјү жұӮ
 .
.
еңЁз ”究еҮҪж•°зҡ„еҸҳеҢ–规еҫӢж—¶пјҢеёёеёёйҒҮеҲ°вҖң  вҖқзӯүж— жі•и§ЈеҶізҡ„жғ…еҶөпјҢеҰӮ
вҖқзӯүж— жі•и§ЈеҶізҡ„жғ…еҶөпјҢеҰӮ  пјҢеҪ“
пјҢеҪ“ 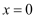 ж—¶е°ұеҮәзҺ°жӯӨжғ…еҶөпјҺйҡҸзқҖеҫ®з§ҜеҲҶзҡ„еҸ‘еұ•еә”з”ЁпјҢж•°еӯҰ家йҮҮеҸ–дәҶеҰӮдёӢзӯ–з•ҘжқҘи§ЈеҶіпјҡеҲҶејҸзҡ„еҲҶеӯҗгҖҒеҲҶжҜҚеқҮдёәеҸҜеҜјеҮҪж•°пјҢеҲҶеҲ«еҜ№еҲҶејҸзҡ„еҲҶеӯҗгҖҒеҲҶжҜҚзҡ„дёӨдёӘеҮҪж•°жұӮеҜјпјҢеҰӮеҜ№еҮҪж•°
ж—¶е°ұеҮәзҺ°жӯӨжғ…еҶөпјҺйҡҸзқҖеҫ®з§ҜеҲҶзҡ„еҸ‘еұ•еә”з”ЁпјҢж•°еӯҰ家йҮҮеҸ–дәҶеҰӮдёӢзӯ–з•ҘжқҘи§ЈеҶіпјҡеҲҶејҸзҡ„еҲҶеӯҗгҖҒеҲҶжҜҚеқҮдёәеҸҜеҜјеҮҪж•°пјҢеҲҶеҲ«еҜ№еҲҶејҸзҡ„еҲҶеӯҗгҖҒеҲҶжҜҚзҡ„дёӨдёӘеҮҪж•°жұӮеҜјпјҢеҰӮеҜ№еҮҪж•°  зҡ„еҲҶеӯҗгҖҒеҲҶжҜҚжұӮеҜјеҫ—еҲ°ж–°еҮҪж•°
зҡ„еҲҶеӯҗгҖҒеҲҶжҜҚжұӮеҜјеҫ—еҲ°ж–°еҮҪж•°  пјҢеҪ“
пјҢеҪ“ 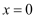 ж—¶пјҢ
ж—¶пјҢ  зҡ„еҖјдёә1пјҢеҲҷ1дёәеҮҪж•°
зҡ„еҖјдёә1пјҢеҲҷ1дёәеҮҪж•°  еңЁ
еңЁ 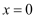 еӨ„зҡ„жһҒйҷҗпјҢж №жҚ®жӯӨжҖқи·ҜпјҢеҮҪж•°
еӨ„зҡ„жһҒйҷҗпјҢж №жҚ®жӯӨжҖқи·ҜпјҢеҮҪж•°  еңЁ
еңЁ 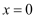 еӨ„зҡ„жһҒйҷҗжҳҜпјҺ
еӨ„зҡ„жһҒйҷҗжҳҜпјҺ
 вҖқзӯүж— жі•и§ЈеҶізҡ„жғ…еҶөпјҢеҰӮ
вҖқзӯүж— жі•и§ЈеҶізҡ„жғ…еҶөпјҢеҰӮ  пјҢеҪ“
пјҢеҪ“ 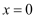 ж—¶е°ұеҮәзҺ°жӯӨжғ…еҶөпјҺйҡҸзқҖеҫ®з§ҜеҲҶзҡ„еҸ‘еұ•еә”з”ЁпјҢж•°еӯҰ家йҮҮеҸ–дәҶеҰӮдёӢзӯ–з•ҘжқҘи§ЈеҶіпјҡеҲҶејҸзҡ„еҲҶеӯҗгҖҒеҲҶжҜҚеқҮдёәеҸҜеҜјеҮҪж•°пјҢеҲҶеҲ«еҜ№еҲҶејҸзҡ„еҲҶеӯҗгҖҒеҲҶжҜҚзҡ„дёӨдёӘеҮҪж•°жұӮеҜјпјҢеҰӮеҜ№еҮҪж•°
ж—¶е°ұеҮәзҺ°жӯӨжғ…еҶөпјҺйҡҸзқҖеҫ®з§ҜеҲҶзҡ„еҸ‘еұ•еә”з”ЁпјҢж•°еӯҰ家йҮҮеҸ–дәҶеҰӮдёӢзӯ–з•ҘжқҘи§ЈеҶіпјҡеҲҶејҸзҡ„еҲҶеӯҗгҖҒеҲҶжҜҚеқҮдёәеҸҜеҜјеҮҪж•°пјҢеҲҶеҲ«еҜ№еҲҶејҸзҡ„еҲҶеӯҗгҖҒеҲҶжҜҚзҡ„дёӨдёӘеҮҪж•°жұӮеҜјпјҢеҰӮеҜ№еҮҪж•°  зҡ„еҲҶеӯҗгҖҒеҲҶжҜҚжұӮеҜјеҫ—еҲ°ж–°еҮҪж•°
зҡ„еҲҶеӯҗгҖҒеҲҶжҜҚжұӮеҜјеҫ—еҲ°ж–°еҮҪж•°  пјҢеҪ“
пјҢеҪ“ 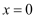 ж—¶пјҢ
ж—¶пјҢ  зҡ„еҖјдёә1пјҢеҲҷ1дёәеҮҪж•°
зҡ„еҖјдёә1пјҢеҲҷ1дёәеҮҪж•°  еңЁ
еңЁ 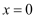 еӨ„зҡ„жһҒйҷҗпјҢж №жҚ®жӯӨжҖқи·ҜпјҢеҮҪж•°
еӨ„зҡ„жһҒйҷҗпјҢж №жҚ®жӯӨжҖқи·ҜпјҢеҮҪж•°  еңЁ
еңЁ 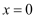 еӨ„зҡ„жһҒйҷҗжҳҜпјҺ
еӨ„зҡ„жһҒйҷҗжҳҜпјҺ
е°Ҷзӣҙзәҝ  пјҡ
пјҡ  пјҢ
пјҢ  пјҡ
пјҡ  пјҲ
пјҲ  пјҢ
пјҢ  пјүдёҺxиҪҙгҖҒyиҪҙеӣҙжҲҗзҡ„е°Ғй—ӯеӣҫеҪўзҡ„йқўз§Ҝи®°дёә
пјүдёҺxиҪҙгҖҒyиҪҙеӣҙжҲҗзҡ„е°Ғй—ӯеӣҫеҪўзҡ„йқўз§Ҝи®°дёә  пјҢеҲҷ
пјҢеҲҷ 
 пјҡ
пјҡ  пјҢ
пјҢ  пјҡ
пјҡ  пјҲ
пјҲ  пјҢ
пјҢ  пјүдёҺxиҪҙгҖҒyиҪҙеӣҙжҲҗзҡ„е°Ғй—ӯеӣҫеҪўзҡ„йқўз§Ҝи®°дёә
пјүдёҺxиҪҙгҖҒyиҪҙеӣҙжҲҗзҡ„е°Ғй—ӯеӣҫеҪўзҡ„йқўз§Ҝи®°дёә  пјҢеҲҷ
пјҢеҲҷ 
е·ІзҹҘеҮҪж•°  пјҲ
пјҲ  пјҢ
пјҢ  пјҢе…¶дёӯ
пјҢе…¶дёӯ  дёәиҮӘ然еҜ№ж•°зҡ„еә•ж•°пјү.
дёәиҮӘ然еҜ№ж•°зҡ„еә•ж•°пјү.
 пјҲ
пјҲ  пјҢ
пјҢ  пјҢе…¶дёӯ
пјҢе…¶дёӯ  дёәиҮӘ然еҜ№ж•°зҡ„еә•ж•°пјү.
дёәиҮӘ然еҜ№ж•°зҡ„еә•ж•°пјү.
-
пјҲ1пјү жұӮеҮҪж•°
 зҡ„еҚ•и°ғйҖ’еўһеҢәй—ҙпјӣ
зҡ„еҚ•и°ғйҖ’еўһеҢәй—ҙпјӣ
-
пјҲ2пјү иӢҘеҮҪж•°
 жңүдёӨдёӘдёҚеҗҢзҡ„йӣ¶зӮ№
жңүдёӨдёӘдёҚеҗҢзҡ„йӣ¶зӮ№  пјҢеҪ“
пјҢеҪ“  ж—¶пјҢжұӮе®һж•°
ж—¶пјҢжұӮе®һж•°  зҡ„еҸ–еҖјиҢғеӣҙ.
зҡ„еҸ–еҖјиҢғеӣҙ.
е·ІзҹҘзӯүжҜ”ж•°еҲ—  зҡ„йҰ–йЎ№дёә2пјҢе…¬жҜ”дёә
зҡ„йҰ–йЎ№дёә2пјҢе…¬жҜ”дёә  пјҢе…¶еүҚ
пјҢе…¶еүҚ  йЎ№е’Ңи®°дёә
йЎ№е’Ңи®°дёә  пјҢеҲҷ
пјҢеҲҷ  .
.
 зҡ„йҰ–йЎ№дёә2пјҢе…¬жҜ”дёә
зҡ„йҰ–йЎ№дёә2пјҢе…¬жҜ”дёә  пјҢе…¶еүҚ
пјҢе…¶еүҚ  йЎ№е’Ңи®°дёә
йЎ№е’Ңи®°дёә  пјҢеҲҷ
пјҢеҲҷ  .
.
еҮҪж•°  зҡ„еӨ§иҮҙеӣҫиұЎдёәпјҲ пјү
зҡ„еӨ§иҮҙеӣҫиұЎдёәпјҲ пјү
 зҡ„еӨ§иҮҙеӣҫиұЎдёәпјҲ пјү
зҡ„еӨ§иҮҙеӣҫиұЎдёәпјҲ пјү
A . 
B .
C . D .
D . 

B .

C .
 D .
D . 
е·ІзҹҘеҮҪж•°  .
.
 .
.
-
пјҲ1пјү еҪ“
 ж—¶пјҢжұӮ
ж—¶пјҢжұӮ  зҡ„еҚ•и°ғеҢәй—ҙпјӣ
зҡ„еҚ•и°ғеҢәй—ҙпјӣ
-
пјҲ2пјү иӢҘе…ідәҺ
 зҡ„дёҚзӯүејҸ
зҡ„дёҚзӯүејҸ  жҒ’жҲҗз«ӢпјҢжұӮaзҡ„еҸ–еҖјиҢғеӣҙ.
жҒ’жҲҗз«ӢпјҢжұӮaзҡ„еҸ–еҖјиҢғеӣҙ.
иӢҘ  еӣҫиұЎдёҠжҒ°еӯҳеңЁдёӨдёӘзӮ№е…ідәҺ
еӣҫиұЎдёҠжҒ°еӯҳеңЁдёӨдёӘзӮ№е…ідәҺ  иҪҙеҜ№з§°пјҢеҲҷе®һж•°
иҪҙеҜ№з§°пјҢеҲҷе®һж•°  зҡ„еҸ–еҖјиҢғеӣҙжҳҜпјҲ пјү
зҡ„еҸ–еҖјиҢғеӣҙжҳҜпјҲ пјү
 еӣҫиұЎдёҠжҒ°еӯҳеңЁдёӨдёӘзӮ№е…ідәҺ
еӣҫиұЎдёҠжҒ°еӯҳеңЁдёӨдёӘзӮ№е…ідәҺ  иҪҙеҜ№з§°пјҢеҲҷе®һж•°
иҪҙеҜ№з§°пјҢеҲҷе®һж•°  зҡ„еҸ–еҖјиҢғеӣҙжҳҜпјҲ пјү
зҡ„еҸ–еҖјиҢғеӣҙжҳҜпјҲ пјү
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
и®ҫеҮҪж•° пјҢ е…¶дёӯ
пјҢ е…¶дёӯ пјҺ
пјҺ
 пјҢ е…¶дёӯ
пјҢ е…¶дёӯ пјҺ
пјҺ
-
пјҲ1пјү и®Ёи®ә
 зҡ„еҚ•и°ғжҖ§пјӣ
зҡ„еҚ•и°ғжҖ§пјӣ
-
пјҲ2пјү еҪ“
 еӯҳеңЁе°ҸдәҺйӣ¶зҡ„жһҒе°ҸеҖјж—¶пјҢиӢҘ
еӯҳеңЁе°ҸдәҺйӣ¶зҡ„жһҒе°ҸеҖјж—¶пјҢиӢҘ пјҢ дё”
пјҢ дё” пјҢ иҜҒжҳҺпјҡ
пјҢ иҜҒжҳҺпјҡ пјҺ
пјҺ
е·ІзҹҘеҮҪж•° еңЁ
еңЁ еӨ„зҡ„еҜјж•°дёә
еӨ„зҡ„еҜјж•°дёә пјҢ еҲҷ
пјҢ еҲҷ пјҲ пјү
пјҲ пјү
 еңЁ
еңЁ еӨ„зҡ„еҜјж•°дёә
еӨ„зҡ„еҜјж•°дёә пјҢ еҲҷ
пјҢ еҲҷ пјҲ пјү
пјҲ пјү
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
жңҖиҝ‘жӣҙж–°
- еҰӮеӣҫжүҖзӨәпјҢеңЁеӨ§еҸЈеҺҡзҺ»з’ғ瓶еҶ…иЈ…е…Ҙе°‘йҮҸзҡ„ж°ҙпјҢ
- Mr. Zhang gave the textbooks to all the pupils except _____
- жҹҗеҚ•дҪҚ200еҗҚиҒҢе·ҘдёӯпјҢ50еІҒд»ҘдёҠпјҲеҗ«50еІҒпјүзҡ„еҚ 10
- вҖ”You see, IвҖҷm poor in maths, you are not good at English
- еңЁжҹҗж¬ЎдәәжүҚдәӨжөҒдјҡдёҠпјҢеә”иҒҳдәәж•°е’ҢжӢӣиҒҳдәәж•°еҲҶ
- жі•еӣҪеӨ§йқ©е‘Ҫжңҹй—ҙпјҢеӣҪзҺӢи·Ҝжҳ“еҚҒе…ӯиў«еӣҡзҰҒпјҢеңЁзӢұ
- 6пјҺ(2011В·еӨ§зәІзүҲе…ЁеӣҪеҚ·)дёӢеҲ—иғҪиҜҙжҳҺжҹҗз»Ҷиғһе·Із»Ҹ
- дёӢеҲ—е…ідәҺеҠӣзҡ„иҜҙжі•дёӯжӯЈзЎ®зҡ„жҳҜAпјҺеҠӣжҳҜзү©дҪ“еҜ№
- е…ідәҺиҝҷзҜҮж–Үз« зҗҶи§Јй”ҷиҜҜзҡ„дёҖйЎ№жҳҜпјҲВ В пјүA.жң¬
- дёӢеӣҫдёәйӘҢиҜҒжңәжў°иғҪе®ҲжҒ’е®ҡеҫӢзҡ„е®һйӘҢиЈ…зҪ®зӨәж„Ҹеӣҫ
- еҸӨд»ЈвҖң银й’ҲйӘҢжҜ’вҖқзҡ„еҺҹзҗҶжҳҜпјҡ4Ag + 2H2S + O2 == 2X
- еҰӮеӣҫпјҢеңЁе№ійқўзӣҙи§’еқҗж Үзі»дёӯпјҢд»ҘдёәйЎ¶зӮ№пјҢиҪҙзҡ„
- дёӢеҲ—иҝҗз®—жӯЈзЎ®зҡ„жҳҜпјҲ пјүпјЎпјҺВ В В В В В В В В В В
- дә’з§°дёәеҗҢеҲҶејӮжһ„дҪ“зҡ„зү©иҙЁдёҚеҸҜиғҪ AпјҺе…·жңүзӣёеҗҢ
- з»„з»Үжі•еӯҰ家жҠҠеҺҶд»Јзҡ„зҪ—马法жұҮзј–жҲҗгҖҠж°‘жі•еӨ§е…Ё
- ---She didnвҖҷt take the medicine last night, did she? --- В
- дёӢеҲ—е…ідәҺзү©иҙЁжҖ§иҙЁзҡ„жҜ”иҫғпјҢдёҚжӯЈзЎ®зҡ„жҳҜпјҲВ В В
- д»Ҡе№ҙпјҢиҒҢеңәе°ҸиҜҙгҖҠжқңжӢүжӢүеҚҮиҒҢи®°гҖӢжҲҗдёәеӣҫд№ҰеёӮ
- йҳ…иҜ»дёӢеҲ—жқҗж–ҷпјҢиҝҗз”ЁжүҖеӯҰзҹҘиҜҶеӣһзӯ”й—®йўҳгҖӮ жқҗ
- жҜӣжіҪ东жӣҫз»ҸжҖ»з»“вҖң1840е№ҙиө·пјҢеҮ д№Һдё–з•ҢжүҖжңү



