极限及其运算 知识点题库
若(1+5x2)n的展开式中各项系数之和是an,(2x3+5)n的展开式中各项的二项式系数之和是bn , 则 的值为
的值为
 的值为
的值为
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知数列 的首项
的首项 不等于0,其前n项的和为
不等于0,其前n项的和为 ,且
,且 ,则
,则 ()
()
 的首项
的首项 不等于0,其前n项的和为
不等于0,其前n项的和为 ,且
,且 ,则
,则 ()
()
A . 0
B .  C . 1
D . 2
C . 1
D . 2
 C . 1
D . 2
C . 1
D . 2
 的值为 ( )
的值为 ( )
A . 0
B . 1
C .  D .
D . 
 D .
D . 
已知 , 则
, 则 =( )
=( )
 , 则
, 则 =( )
=( )
A . 4
B . -8
C . 0
D . 8
曲线  在点(1,-1)处的切线方程为( ).
在点(1,-1)处的切线方程为( ).
 在点(1,-1)处的切线方程为( ).
在点(1,-1)处的切线方程为( ).
A . y=x-2
B . y=x
C . y=x+2
D . y=-x-2
设n∈N* , 圆  的面积为Sn , 则
的面积为Sn , 则 = .
= .
 的面积为Sn , 则
的面积为Sn , 则 = .
= .
若 
 =2,则a+b=.
=2,则a+b=.

 =2,则a+b=.
=2,则a+b=.
已知函数  .
.
 .
.
-
(1) 当
 时,求
时,求  在
在  ,
,  (1)
(1)  处的切线方程;
处的切线方程;
-
(2) 当
 ,
,  时,
时,  恒成立,求
恒成立,求  的取值范围.
的取值范围.
定义:若函数  对任意的
对任意的  ,都有
,都有  成立,则称
成立,则称  为
为  上的“淡泊”函数.
上的“淡泊”函数.
 对任意的
对任意的  ,都有
,都有  成立,则称
成立,则称  为
为  上的“淡泊”函数.
上的“淡泊”函数.
-
(1) 判断
 是否为
是否为  上的“淡泊”函数,说明理由;
上的“淡泊”函数,说明理由;
-
(2) 是否存在实数
 ,使
,使  为
为  上的“淡泊”函数,若存在,求出
上的“淡泊”函数,若存在,求出  的取值范围;不存在,说明理由;
的取值范围;不存在,说明理由;
-
(3) 设
 是
是  上的“淡泊”函数(其中
上的“淡泊”函数(其中  不是常值函数),且
不是常值函数),且  ,若对任意的
,若对任意的  ,都有
,都有  成立,求
成立,求  的最小值.
的最小值.
已知函数  .
.
 .
.
-
(1) 若
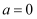 ,求
,求  的最小值;
的最小值;
-
(2) 若
 在
在  上单调递增,求
上单调递增,求  的取值范围;
的取值范围;
-
(3) 若
 ,
,  求证:
求证:  .
.
已知函数  ,若函数
,若函数  只有一个零点
只有一个零点  ,且
,且  ,则实数
,则实数  的取值范围.
的取值范围.
 ,若函数
,若函数  只有一个零点
只有一个零点  ,且
,且  ,则实数
,则实数  的取值范围.
的取值范围.
若过点(a,b)可以作曲线y=ex的两条切线,则( )
A . eb<a
B . ea<b
C . 0<a<eb
D . 0<b<ea
过定点  作曲线
作曲线  的切线,恰有2条,则实数
的切线,恰有2条,则实数  的取值范围是.
的取值范围是.
 作曲线
作曲线  的切线,恰有2条,则实数
的切线,恰有2条,则实数  的取值范围是.
的取值范围是.
已知函数  .
.
 .
.
-
(1) 讨论函数
 的单调性;
的单调性;
-
(2) 当
 时,若曲线
时,若曲线  与曲线
与曲线  存在唯一的公切线,求实数
存在唯一的公切线,求实数  的值;
的值;
-
(3) 当
 时,不等式
时,不等式  恒成立,求实数
恒成立,求实数  的取值范围.
的取值范围.
已知函数  .
.
 .
.
-
(1) 讨论
 的单调性;
的单调性;
-
(2) 若
 只有1个零点
只有1个零点  ,且
,且  ,求
,求  的取值范围;
的取值范围;
-
(3) 当
 时,是否存在正整数k,使得关于x的方程
时,是否存在正整数k,使得关于x的方程  有解?如果存在,求出k的值;如果不存在,说明理由.
有解?如果存在,求出k的值;如果不存在,说明理由.
已知  ,直线
,直线  为曲线
为曲线  在
在  处的切线,直线
处的切线,直线  与曲线
与曲线  相交于点
相交于点  且
且  .
.
 ,直线
,直线  为曲线
为曲线  在
在  处的切线,直线
处的切线,直线  与曲线
与曲线  相交于点
相交于点  且
且  .
.
-
(1) 求
 的取值范围;
的取值范围;
-
(2) (i)证明:
 ;
; (ii)证明:
 .
.
若函数 存在最小值,则实数a的取值范围是.
存在最小值,则实数a的取值范围是.
 存在最小值,则实数a的取值范围是.
存在最小值,则实数a的取值范围是.
已知函数 , 直线
, 直线 , 点
, 点 在函数
在函数 图像上,则以下说法正确的是( )
图像上,则以下说法正确的是( )
 , 直线
, 直线 , 点
, 点 在函数
在函数 图像上,则以下说法正确的是( )
图像上,则以下说法正确的是( )
A . 若直线l是曲线 的切线,则
的切线,则 B . 若直线l与曲线
B . 若直线l与曲线 无公共点,则
无公共点,则 C . 若
C . 若 , 则点P到直线l的最短距离为
, 则点P到直线l的最短距离为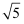 D . 若
D . 若 , 当点P到直线l的距离最短时,
, 当点P到直线l的距离最短时,
 的切线,则
的切线,则 B . 若直线l与曲线
B . 若直线l与曲线 无公共点,则
无公共点,则 C . 若
C . 若 , 则点P到直线l的最短距离为
, 则点P到直线l的最短距离为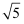 D . 若
D . 若 , 当点P到直线l的距离最短时,
, 当点P到直线l的距离最短时,
已知函数 , 若
, 若 , 则
, 则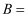 ( )
( )
 , 若
, 若 , 则
, 则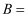 ( )
( )
A . 1
B . 2
C . 3
D . 4
函数 的大致图象是( )
的大致图象是( )
 的大致图象是( )
的大致图象是( )参考公式:对于函数 , 若
, 若 与
与 在
在 处可导,且
处可导,且 , 则
, 则 .
.
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 用适当的数字和符号填写: (1)三个氢原子�
- 唐太宗在位时曾说:“国家本置中书、门下以
- 以“文化交融和谐动脉”为主题的第六届海峡
- 科研人员对某草原一种野生动物的种群进行研
- ---- I did well in the English exam last week. ---- I did __
- 若20g密度为dg/cm3的硝酸钙溶液里含1gCa2+,则NO3
- 读下图,回答下列问题。 (1)说出图中,祁
- 2010年7月31日,《海南省实施<中华人民共和
- 若向日葵的某种细胞间隙的渗透压为A,细胞
- 一起重机的钢绳由静止开始匀加速提起质量为
- 如图,点、、是上的三点,. (1)求证:平分
- 下列各选项中加线字的解释错误的一项是 ①
- 在答题卷横线上填入相应的诗句。(每空1分
- 某人欲估算飞机着陆时的速度,他假设飞机着
- 如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且
- 当一个人的情绪不好时,应该采取一些方法进
- 19.仿照下面句子,另写两句富有意蕴的句子
- “其目的不是同共产主义作斗争,而是同经
- 函数的最大值为 ;
- 绘制等高线地形图时,选择等高距的主要依据



