极限及其运算 知识点题库
已知函数 , 图像的最高点从左到右依次记为
, 图像的最高点从左到右依次记为 , 函数
, 函数 的图像与
的图像与 轴的交点从左到右依次记为
轴的交点从左到右依次记为 , 设
, 设 , 则
, 则 ( )
( )
A .  B . -
B . - C .
C .  D . -
D . -
 B . -
B . - C .
C .  D . -
D . -
若 存在,则实数x的取值范围是( )
存在,则实数x的取值范围是( )
 存在,则实数x的取值范围是( )
存在,则实数x的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数 f(x) 在 x=1 处的导数为1,则 ( )
( )
 ( )
( )
A . 3
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
设函数 y=f(x) ,当自变量由 x0 变到  时,函数的改变量.
时,函数的改变量.
 时,函数的改变量.
时,函数的改变量.
在等比数列{an}中,a1>1,且前n项和Sn满足 Sn=
Sn= , 那么a1的取值范围是( )
, 那么a1的取值范围是( )
 Sn=
Sn= , 那么a1的取值范围是( )
, 那么a1的取值范围是( )
A . (1,+∞)
B . (1,4)
C . (1,2)
D . (1, )
)
 )
)
设函数f(x)在x=2处导数存在,则 =( )
=( )
 =( )
=( )
A . ﹣2f′(2)
B . 2f′(2)
C . ﹣ f′(2)
D .
f′(2)
D .  f′(2)
f′(2)
 f′(2)
D .
f′(2)
D .  f′(2)
f′(2)
对于函数  ,若存在区间
,若存在区间  ,当
,当  时的值域为
时的值域为  ,则称
,则称  为
为  倍值函数.若
倍值函数.若  是
是  倍值函数,则实数
倍值函数,则实数  的取值范围是( )
的取值范围是( )
 ,若存在区间
,若存在区间  ,当
,当  时的值域为
时的值域为  ,则称
,则称  为
为  倍值函数.若
倍值函数.若  是
是  倍值函数,则实数
倍值函数,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  ,则
,则  .
.
 ,则
,则  .
.
已知函数  有且仅有
有且仅有  个零点,则实数
个零点,则实数  的取值范围为.
的取值范围为.
 有且仅有
有且仅有  个零点,则实数
个零点,则实数  的取值范围为.
的取值范围为.
已知函数  的图像与直线
的图像与直线  只有一个交点,则
只有一个交点,则  的取值范围是( )
的取值范围是( )
 的图像与直线
的图像与直线  只有一个交点,则
只有一个交点,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设函数  在
在  上可导,且
上可导,且  为奇函数,则
为奇函数,则  ( )
( )
 在
在  上可导,且
上可导,且  为奇函数,则
为奇函数,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 .
.
已知数列  的通项公式为
的通项公式为  ,
,  ,其前n项和为
,其前n项和为  ,则
,则  .
.
 的通项公式为
的通项公式为  ,
,  ,其前n项和为
,其前n项和为  ,则
,则  .
.
已知函数  .
.
 .
.
-
(1) 判断并证明
 在
在  的单调性;
的单调性;
-
(2) 已知a为正实数,且对于任意
 ,都有
,都有  恒成立,求正实数a的取值范围.
恒成立,求正实数a的取值范围.
已知 , 记
, 记 表示
表示 中的最大值,
中的最大值, 表示
表示 中的最小值,若
中的最小值,若  , 数列
, 数列 和
和 满足
满足
 , 则下列说法中正确的是( )
, 则下列说法中正确的是( )
 , 记
, 记 表示
表示 中的最大值,
中的最大值, 表示
表示 中的最小值,若
中的最小值,若  , 数列
, 数列 和
和 满足
满足
 , 则下列说法中正确的是( )
, 则下列说法中正确的是( )
A . 若 , 则存在正整数
, 则存在正整数 , 使得
, 使得 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 , 则存在正整数
, 则存在正整数 , 使得
, 使得
 , 则存在正整数
, 则存在正整数 , 使得
, 使得 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 , 则存在正整数
, 则存在正整数 , 使得
, 使得
已知函数 .
.
 .
.
-
(1) 若
 有两个极值点,求实数a的取值范围;
有两个极值点,求实数a的取值范围;
-
(2) 当
 时,证明:
时,证明: .
.
已知  为奇函数,当
为奇函数,当  时,
时,  ,且
,且  关于直线
关于直线  对称,设
对称,设  的正数解依次为
的正数解依次为  、
、  、
、  、
、  、
、  、
、  ,则
,则 
 为奇函数,当
为奇函数,当  时,
时,  ,且
,且  关于直线
关于直线  对称,设
对称,设  的正数解依次为
的正数解依次为  、
、  、
、  、
、  、
、  、
、  ,则
,则 
已知 , 设函数
, 设函数 .
.
 , 设函数
, 设函数 .
.
-
(1) 当
 时,若函数
时,若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
-
(2) 若对任意实数
 , 函数
, 函数 均有零点,求实数
均有零点,求实数 的最大值;
的最大值;
-
(3) 若函数
 有两个零点
有两个零点 , 证明:
, 证明: .
.
已知 是函数
是函数 的导函数,若
的导函数,若 , 则
, 则 ( )
( )
 是函数
是函数 的导函数,若
的导函数,若 , 则
, 则 ( )
( )
A . 8
B . 4
C . 2
D . -2
若函数 在
在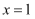 处的导数为2,则
处的导数为2,则 ( )
( )
 在
在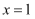 处的导数为2,则
处的导数为2,则 ( )
( )
A . 2
B . 1
C .  D . 6
D . 6
 D . 6
D . 6
最近更新
- 下图中的a图为“某大陆局部地域自然带分布
- 能发生消去反应且产物存在同分异构的是(
- 下列分子的电子式书写正确的是:
- 关于汽车涉及到的一些物理知识,下列说法中
- (2019·福建中考模拟)如图,直线y=-x+b与双曲
- 下列计算结果正确的是. ( ) A. B.
- 下列物质中,不能与金属钠反应并生成氢气
- 如图为细胞的组成成分图,下列说法不正确的
- 若一个扇形的周长与面积的数值相等,则该扇
- 下列说法正确的是( ) A.二氧化硫的催化
- 2010年5月15日是国际家庭日,在全国妇联发布
- 俄国化学家门捷列夫在总结前人经验的基础上
- There is such a problem _____ we all should _____.
- (04江苏卷)让杂合高茎豌豆自交,后代中出
- 设集合A=,B=,若,则实数a的取值范围是___
- 27.“以天国的理想作为现实奋斗的目标
- 有人说:群众最有创造力。紧密联系群众,一
- Free and secure accommodation, no bills and even the odd hom
- 若A表示四件产品中至少有一件是废品的事件,B
- 单词短语翻译:(共15题) 按所给中文意思或



