极限及其运算 知识点题库
设f′(a)=4,则  =( )
=( )
 =( )
=( )
A . 4
B . 8
C . 12
D . ﹣4
设f(x)在x=x0处可导,且  =1,则f′(x0)=( )
=1,则f′(x0)=( )
 =1,则f′(x0)=( )
=1,则f′(x0)=( )
A . 1
B . 3
C .  D . 0
D . 0
 D . 0
D . 0
若  =1,则f′(x0)等于( )
=1,则f′(x0)等于( )
 =1,则f′(x0)等于( )
=1,则f′(x0)等于( )
A . 2
B . ﹣2
C .  D .
D . 
 D .
D . 
过曲线  上一点
上一点  及邻近一点
及邻近一点  作割线,则当
作割线,则当  时割线的斜率为( )
时割线的斜率为( )
 上一点
上一点  及邻近一点
及邻近一点  作割线,则当
作割线,则当
A .  B .
B .  C . 1
D .
C . 1
D . 
 B .
B .  C . 1
D .
C . 1
D . 
在曲线  上取一点
上取一点  及附近一点
及附近一点  ,
,
 上取一点
上取一点  及附近一点
及附近一点  ,
,求:
-
(1)
 ;
;
-
(2)
 .
.
已知函数  .
.
 .
.
-
(1) 若
 ,求曲线在
,求曲线在 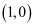 点处的切线方程;
点处的切线方程;
-
(2) 若曲线
 与直线
与直线 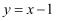 只有一个交点,求实数
只有一个交点,求实数  的取值范围.
的取值范围.
 .
.
若函数  在
在  处的导数为
处的导数为  ,则
,则  为( )
为( )
 在
在  处的导数为
处的导数为  ,则
,则  为( )
为( )
A .  B .
B .  C .
C .  D . 0
D . 0
 B .
B .  C .
C .  D . 0
D . 0
若不等式ex﹣ax2﹣  ax>0对于任意的x∈R恒成立,则实数a的取值范围是( )
ax>0对于任意的x∈R恒成立,则实数a的取值范围是( )
 ax>0对于任意的x∈R恒成立,则实数a的取值范围是( )
ax>0对于任意的x∈R恒成立,则实数a的取值范围是( )
A . (  ,0]
B . [0,
,0]
B . [0,  )
C . (0,
)
C . (0,  )
D . (﹣∞,
)
D . (﹣∞,  )
)
 ,0]
B . [0,
,0]
B . [0,  )
C . (0,
)
C . (0,  )
D . (﹣∞,
)
D . (﹣∞,  )
)

若  ,则
,则  .
.
 ,则
,则  .
.
设Pn(xn , yn)是直线3x+y=  (n∈N*)与圆x2+y2=5在第四象限的交点,则极限
(n∈N*)与圆x2+y2=5在第四象限的交点,则极限  =.
=.
 (n∈N*)与圆x2+y2=5在第四象限的交点,则极限
(n∈N*)与圆x2+y2=5在第四象限的交点,则极限  =.
=.
 .
.
已知函数  在
在  处取得极大值.
处取得极大值.
 在
在  处取得极大值.
处取得极大值.
-
(1) 求
 的值;
的值;
-
(2) 若
 ,证明:
,证明:  有且只有3个零点.
有且只有3个零点.
已知  等于( )
等于( )
 等于( )
等于( )
A . 1
B . -1
C . 3
D . 6
已知数列  ,
,  ,
,  的前n项和为
的前n项和为  .
.
 ,
,  ,
,  的前n项和为
的前n项和为  .
.
-
(1) 若
 为等比数列,
为等比数列,  ,求
,求  ;
;
-
(2) 若
 为等差数列,公差为d,对任意
为等差数列,公差为d,对任意  ,均满足
,均满足  ,求d的取值范围.
,求d的取值范围.
某机构为了解市民对交通的满意度,随机抽取了100位市民进行调查结果如下:回答“满意”的人数占总人数的一半,在回答“满意”的人中,“上班族”的人数是“非上班族”人数的 ;在回答“不满意”的人中,“非上班族”占
;在回答“不满意”的人中,“非上班族”占 .
.
 ;在回答“不满意”的人中,“非上班族”占
;在回答“不满意”的人中,“非上班族”占 .
.附:
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: , 其中
, 其中 .
.
-
(1) 请根据以上数据填写下面
 列联表,并依据小概率值
列联表,并依据小概率值 的独立性检验,分析能否认为市民对于交通的满意度与是否为上班族存关联?
的独立性检验,分析能否认为市民对于交通的满意度与是否为上班族存关联?满意
不满意
合计
上班族
非上班族
合计
-
(2) 为了改善市民对交通状况的满意度,机构欲随机抽取部分市民做进一步调查.规定:抽样的次数不超过
 , 若随机抽取的市民属于不满意群体,则抽样结束;若随机抽取的市民属于满意群体,则继续抽样,直到抽到不满意市民或抽样次数达到
, 若随机抽取的市民属于不满意群体,则抽样结束;若随机抽取的市民属于满意群体,则继续抽样,直到抽到不满意市民或抽样次数达到 时,抽样结束.
时,抽样结束.(i)若
 , 写出
, 写出 的分布列和数学期望;
的分布列和数学期望;(ii)请写出
 的数学期望的表达式(不需证明),根据你的理解说明
的数学期望的表达式(不需证明),根据你的理解说明 的数学期望的实际意义.
的数学期望的实际意义.
已知函数 .
.
 .
.
-
(1) 讨论函数
 的零点个数;
的零点个数;
-
(2) 若函数
 存在两个不同的零点
存在两个不同的零点 , 证明:
, 证明: .
.
若曲线 与曲线
与曲线 有公切线,则
有公切线,则 的取值范围是.
的取值范围是.
 与曲线
与曲线 有公切线,则
有公切线,则 的取值范围是.
的取值范围是.
已知函数 , 则
, 则 ( )
( )
 , 则
, 则 ( )
( )
A . 12
B . 6
C . 3
D . 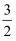
最近更新
- 科学家已发现的一种新型氢分子,其化学式为
- I won’t tell the student the answer to the math problem un
- 某种产品的广告费支出x与销售额y(单位:百万
- 小红通过查阅资料得知:红色、蓝色、紫色的
- 关于带电粒子在匀强磁场中的运动,下列说法
- 在改革开放中,经过三次思想解放,我们先后
- 下列各组分子中,都属于含极性键的非极性分
- 下列离子在溶液中可以大量共存的是(
- “我们唱着东方红,当家作主站起来。”这首
- 在一条直线上依次有A、B、C三个海岛,某海巡
- 下列各组离子,一定能在指定环境中大量共
- (2011年浙江杭州, 30题)为了减轻酸雨的危
- The bad weather only _________ our difficulties. A. added u
- 芳香族化合物A的分子式为C7H6O2,将它与NaHCO3
- 有关光的传播和反射,下列说法正确的有(
- 列何种技术能有效地打破物种的界限,定向地
- 读下表,完成下列问题。 测量位置距地面的
- It is generally accepted that the profit-sharing plan is
- 如图,正方体ABCD—A1B1C1D1,则下列四个命题:
- The child was almost _______________ from the outside worl















