八年级(初二)数学下学期下册试题
绵州大剧院举行专场音乐会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款,某校有4名老师与若干名(不少于4人)学生听音乐会.
-
(1) 设学生人数为x(人),付款总金额为y(元),分别建立两种优惠方案中y与x的函数关系式;
-
(2) 请计算并确定出最节省费用的购票方案.
如图,正方形ABCD的边长为3,E在BC上,且BE=2,P在BD上,则PE+PC的最小值为( )

A .  B .
B . 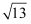 C .
C .  D .
D . 
 B .
B . 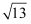 C .
C .  D .
D . 
甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过300元后的价格部分打7折.
-
(1) 以
 (单位:元)表示商品原价,
(单位:元)表示商品原价,  (单位:元)表示购物金额,分别就两家商场的让利方式写出
(单位:元)表示购物金额,分别就两家商场的让利方式写出  与
与  的函数解析式;
的函数解析式;
-
(2) 在同一直角坐标系中画出(1)中函数的图象;
-
(3) 春节期间如何选择这两家商场去购物更省钱?
某学校组织八年级学生在网络上参加传染病防控知识竞赛,试卷共有  道选择题,每题
道选择题,每题  分,如图所示的是从甲、乙两班各随机抽取的
分,如图所示的是从甲、乙两班各随机抽取的  名学生的得分情况.
名学生的得分情况.
 道选择题,每题
道选择题,每题  分,如图所示的是从甲、乙两班各随机抽取的
分,如图所示的是从甲、乙两班各随机抽取的  名学生的得分情况.
名学生的得分情况. 

-
(1) 利用图中提供的信息,补全下表:
班级
平均数/分
中位数/分
众数/分
甲班

乙班


-
(2) 若把
 分以上(含
分以上(含  分)记为“优秀”,已知两班各有
分)记为“优秀”,已知两班各有 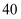 名学生,请估计两班各有多少名学生成绩为优秀.
名学生,请估计两班各有多少名学生成绩为优秀.
如图已知  ,
,  于点C,
于点C,  于点D交HG于点K.
于点D交HG于点K.  ,
,  ,
,  .
.
 ,
,  于点C,
于点C,  于点D交HG于点K.
于点D交HG于点K.  ,
,  ,
,  .
. 
-
(1) 若
 ,点M是CD上一点,当点M到点A和点B的距离相等时,求CM的长;
,点M是CD上一点,当点M到点A和点B的距离相等时,求CM的长;
-
(2) 若
 ,点P是HG上一点,点Q是EF上一点,连接AP,PQ,QB,求
,点P是HG上一点,点Q是EF上一点,连接AP,PQ,QB,求  的最小值.
的最小值.
数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得 , 对角线
, 对角线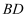 长为
长为 , 改变教具的形状成为图2所示的正方形,则正方形的对角线长为( )
, 改变教具的形状成为图2所示的正方形,则正方形的对角线长为( )
 , 对角线
, 对角线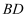 长为
长为 , 改变教具的形状成为图2所示的正方形,则正方形的对角线长为( )
, 改变教具的形状成为图2所示的正方形,则正方形的对角线长为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y= 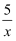 (x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2的值为.
(x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2的值为.
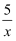 (x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2的值为.
(x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2的值为. 
如图,已知二次函数y=x2-4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
(1)求直线BC的解析式;
(2)点D是在直线BC下方的抛物线上的一个动点,当△BCD的面积最大时,求D点坐标.
为比较营养液A和营养液B对某种小西红柿产量的影响,甲、乙两个生物小组各选取了10株长势相近的小西红柿秧苗进行对照实验,甲组使用营养液A,乙组使用营养液B.将每株的产量记录整理,并绘制了如下两个条形图.

解答下列问题:
-
(1) 甲组产量的众数为,乙组产量的中位数为;
-
(2) 经过计算发现两组产量的平均数接近,为了使产量更稳定,则应选择营养液(填“A”或“B”);
-
(3) 产量30个及以上为秧苗长势良好.现在选用第(2)问推荐的营养液培育100株秧苗,请估计长势良好的大约为株.
综合与探究:如图,在平面直角坐标系中,直线l1:  分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:  交于A.
交于A.
 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:  交于A.
交于A. 
-
(1) 求出点A的坐标.
-
(2) 当y1<y2时,直接写出x的取值范围.
-
(3) 在平面内是否存在点Q,使以O、C、A、Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
如图所示,长方形ABCD中,AB=6cm,BC=8cm,将长方形对折,使B点与D点重合,它的折痕为EF,求图中CE的长.

已知等腰△OAB的面积为3,其底边OB在x轴上,且点B的坐标为(2,0),点A在第四象限,则OA所在的直线的解析式为( )
A . y=3x
B . y=﹣3x
C . y=  x
D . y=﹣
x
D . y=﹣  x
x
 x
D . y=﹣
x
D . y=﹣  x
x
若一组数据1,2,x,4的众数是1,则这组数据的方差为 .
如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

-
(1) 线段AB,BC,AC的长分别为AB=,BC=,AC=;
-
(2) 折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.请从下列A、B两题中任选一题作答,我选择题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的5名选手的复赛成绩如图所示。

-
(1) 根据图示补全下表;
平均数(分)
中位数(分)
众数(分)
A队
83
85
B队
95
-
(2) 结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好;
-
(3) 计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定。
直线y=2x﹣6向上平移3个单位后得到的直线是 .
小明随机抽查了九年级(2)班9位同学一周写数学作业的时间,分别为6,4,6,5,6,7,6,6,8(单位:h).则估计本班大多数同学一周写数学作业的时间约为( )
A . 4h
B . 5h
C . 6h
D . 7h
直线 与y轴的交点坐标为( )
与y轴的交点坐标为( )
 与y轴的交点坐标为( )
与y轴的交点坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知一组数据:1,4,x,2,5,7,若这组数据的众数为2,则这组数据的平均数、中位数分别是( )
A . 3.5,2
B . 3.5,3
C . 4,3
D . 3.5,4
如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD长为( )

A . 2
B . 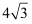 C .
C .  D . 4
D . 4
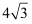 C .
C .  D . 4
D . 4
最近更新
- 小明想利用一块电流表和阻值已知的电阻R0测量未知电阻RX的阻值。小明选择了满足这个实验要求的实验器材,并连接了部分实验电
- 某同学用托盘天平称量固体物质时;把固体物质放在右盘,砝码放在左盘,称得固体物质的质量为10.8 g(1克以下用游码),如
- 20世纪20年代的中国,人民已经醒来。但是,正如鲁迅所说的“人生最痛苦的事,是梦醒了发现无处可走”。下列为中国人民指明了
- The mountain is covered with heavy snow and it is ______ onl
- 若要检验酒精中是否含有少量水,可选用的试剂是A.生石灰 B.无水硫
- 我国已经初步建立起全面的行政监督体系。下列选项中属于行政系统内部监督的是 A.公共媒体的监督
- 如图所示的四种情景中,所使用的杠杆属于费力杠杆的是 ]
- 山东省教育厅日前发出通知,要求中小学开展经典诵读时加以甄别,尤其不可要求全文背诵《三字经》等。对传统启蒙读物的正确认识是
- 阅读下列材料,回答下列问题。 材料一 方里而井,井九百亩,其中为公田。八家皆私百亩,同养公田;公事毕,然后敢治私事。 —
- 一定能在下列溶液中大量共存的离子组是( ) A.水电离产生的c(H+)=1×10-12mol/L溶液:NH4+、N
- He is too careless and he _______ keys. A. always lost B. al
- 一种彩灯工作时的额定电压是36V,如果要用干电池作电源,至少要_____节干电池_____联;如果接在220V的家庭电路
- 请按要求修改下面一段话。 乘车时希望能有个座位,这无可厚非,坐着毕竟比站着要舒服。但是,也应该看到,那些年纪大的老人,(
- (一)阅读刘禹锡的《赏牡丹》 一诗,完成第7 题。(6 分)庭前芍药妖无格,池上芙蕖净少情。唯有牡丹真国色,花开时节动京
- 有关文学常识的表述,错误的一项是( ) A.把长篇小说分成若干章节,每一章节叫做“一回”,用这种形式写成的小说叫做
- 阅读下面的古一首宋词,回答后面的问题。(4分)破阵子·为陈同甫赋壮词以寄之 辛弃疾醉里挑灯看剑,梦回吹角连营。八百
- 下列哪些物质不是在细胞核中合成的( ) A.染色体中的蛋白质 B.染色体中DNA C.与核
- X、Y、Z三种短周期主族元素,原子半径的大小为r(X)>r(Y)>r(Z),X和Y同周期,Y和Z同主族。下列
- 下表为1851年欧美主要国家城市和农村人口的统计,从此表中的史实来看最能说明的问题是 A.工业革命促进人口由农村向城市流
- 旋转的基本性质是:_________.



