八年级(初二)数学下学期下册试题
甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
|
A工地 |
B工地 |
|
|
甲工程队 |
800元 |
750元 |
|
乙工程队 |
600元 |
570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
-
(1) 求y与x之间的函数关系式;
-
(2) 请判断y是否能等于62000,并说明理由.
菱形的对角线长分别是5cm、12cm,则该菱形的面积为
已知正比例函数y=(2a-1)x,如果y的值随着x的值增大而减小,则a的取值范围是
某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
-
(1) 如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
-
(2) 当所挂物体的质量为10千克时,弹簧的长度是多少?
如图,以两条直线l1 , l2的交点坐标为解的方程组是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
一组数据4,5,a,7,9的平均数是6,则这组数据的中位数是.
如图,请在下列四个论断中选出两个作为条件,推出四边形ABCD是平行四边形,并予以证明(写出一种即可).

①AD∥BC;②AB=CD;③∠A=∠C;④∠B+∠C=180°.
已知:在四边形ABCD中,.
求证:四边形ABCD是平行四边形.
下列根式中,与 是同类二次根式的是( )
是同类二次根式的是( )
 是同类二次根式的是( )
是同类二次根式的是( )
A .  B .
B .  C .
C . 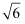 D .
D . 
 B .
B .  C .
C . 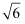 D .
D . 
已知:在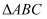 中,
中, 是
是 边上的中线,点
边上的中线,点 是
是 的中点;过点
的中点;过点 作
作 , 交
, 交 的延长线于
的延长线于 , 连接
, 连接 .
.
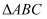 中,
中, 是
是 边上的中线,点
边上的中线,点 是
是 的中点;过点
的中点;过点 作
作 , 交
, 交 的延长线于
的延长线于 , 连接
, 连接 .
.
-
(1) 求证:四边形
 是平行四边形;
是平行四边形;
-
(2) 当
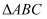 分别满足什么条件时,四边形
分别满足什么条件时,四边形 是菱形;四边形
是菱形;四边形 是矩形,并说明理由.
是矩形,并说明理由.
对于函数y=-k2x(k是常数,k≠0)的图象,下列说法不正确的是( )
A . 是一条直线
B . 过点(  ,-k)
C . 经过第一、三象限或第二、四象限
D . y随着x的增大而减小
,-k)
C . 经过第一、三象限或第二、四象限
D . y随着x的增大而减小
 ,-k)
C . 经过第一、三象限或第二、四象限
D . y随着x的增大而减小
,-k)
C . 经过第一、三象限或第二、四象限
D . y随着x的增大而减小
如果下列各组数是三角形的三边长,那么能组成直角三角形的一组数是( )
A .  ,
, 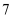 ,
, 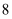 B .
B .  ,
,  ,
, 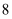 C .
C .  ,
,  ,
,  D .
D .  ,
,  ,
, 
 ,
, 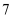 ,
, 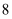 B .
B .  ,
,  ,
, 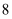 C .
C .  ,
,  ,
,  D .
D .  ,
,  ,
, 
在“看图说故事”活动中,栽学习小组结合图象设计了一个问题情境.

已知小明家、小刚家、体育馆、图书馆依次在同一条直线上.小明从家出发,匀速骑行  到达体育馆;在体有馆停留一段时间后,匀速步行
到达体育馆;在体有馆停留一段时间后,匀速步行  到达小刚家;在小刚家停留
到达小刚家;在小刚家停留  后,两人一起匀速骑行
后,两人一起匀速骑行  后到达图书馆;在图书馆停留
后到达图书馆;在图书馆停留  后,两人一起匀速骑行返回各自的家中.给出的图象反映了这个过程中小明离开家的距离
后,两人一起匀速骑行返回各自的家中.给出的图象反映了这个过程中小明离开家的距离  与离开家的时间
与离开家的时间  之间的对应关系.
之间的对应关系.
请根据相关信息,解答下列问题:
-
(1) 填表:
小明离开家的时间/h
0.1
0.4
0.5
2.5
3.3
小明离开家的距离/

1.2
5
-
(2) 填空:
①小明家与小刚家之间的距离为
 ;
;②小明从体育馆到小刚家的步行速度为
 ;
;③两人从小刚家到图书馆的骑行速度为
 ;
;④当小明离开家的距高为
 时,他离开家的时间为h .
时,他离开家的时间为h . -
(3) 当
 时,请直接写出y关于x的函数解析式.
时,请直接写出y关于x的函数解析式.
如图在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连结EF,则∠E+∠F=

如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是( )

A . 4.5
B . 5
C . 5.5
D . 6
在  中,
中, 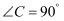
 中,
中, 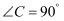
-
(1) 如图①,已知
 ,求
,求  的长;
的长; 
-
(2) 如图②,
 ,垂足为点
,垂足为点  ,已知
,已知  ,求
,求  的长.
的长. 
如图,两个一次函数y=kx+b与y=mx+n的图象分别为直线l1和l2 , l1与l2交于点A(1,p),l1与x轴交于点B(-2,0),l2与x轴交于点C(4,0),则不等式组0<mx+n<kx+b的解集为.

下面说法中,正确的是( )
A . 有一个角是直角的四边形是矩形
B . 两条对角线相等的四边形是矩形
C . 两条对角线互相垂直的四边形是矩形
D . 四个角都是直角的四边形是矩形
如果三角形有一边上的中线长恰好等于这边的长,则称这个三角形为“美好三角形”.
-
(1) 等边△ABC的边长为2,△ABC是“美好三角形”吗?请说明理由;
-
(2) 已知Rt△ABC是“美好三角形”,∠C=90°,AC=2
 ,求BC的长.
,求BC的长.
计算:
-
(1) 5
 +
+ 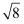 ﹣7
﹣7 
-
(2)
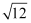 ×(
×(  +3
+3 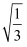 ﹣
﹣ 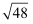 )
)
若  =10,则x的值等于( )
=10,则x的值等于( )
 =10,则x的值等于( )
=10,则x的值等于( )
A . 4
B . ±2
C . 2
D . ±4
最近更新
- 书面表达 爱悄深,母爱无价;学会感恩,学会回报。某英语网站举办以“My mother”为题的英语征文活动。请你根据下列思
- Many people do not realize the importance of health t
- 为测树的高度,在水平地面上选取A、B两点(点A、B及树的底部在同一直线上),从A、B两点分别测得树尖的仰角为30°,45
- 下列物质的性质属于化学性质的是 ( ) A. 颜
- I know there are many interesting and useful jobs but I woul
- 科学文化修养和思想道德修养是一个人应当同时具备的基本素养。下列古语中蕴含二者关系的有 ①“富贵不能淫,贫贱不能移,威武不
- 下列史实中,表明帝国主义在一定程度上形成宰割中国同盟的有 ①三国干涉还辽 ②“门户开放”政策推行③第二次鸦片战争 ④八
- 下列有机物分子中,所有原子不可能在同一平面内的是 ( )
- 1985年,国务院在《关于国有企业工资改革问题的通知》中规定,企业工资总额同经济效益浮动的比率,一般是上缴税利总额增长1
- I’m thinking about going to Germany this summer and I need
- The investor seemed aboutthe idea of exploiting this
- 下列有关物质鉴别的说法中,正确的一组是() A.只用Ba(OH)2溶液即可鉴别(NH4)2CO3、(NH4)2SO4、N
- 17.将要上钩的鱼,会被岸上的说话声吓跑,表明水能够__________。
- -- How long______ you __________England , Sue ? --Since tw
- 研究人员只以某种植物种子饲喂三只年龄、生理状态相同的同种实验鼠,一个月之后,测定实验鼠血液中的甲状腺激素和促甲状腺激素的
- 参照示例,从历史名人中任选两个,根据示例仿写两个句子。 示例:孔子 一代圣贤,在纷乱纠杂的学派潮流中,仍认清人生的真
- 分解因式 x5+x+1;
- 下列图像表示Al3+与AlO2-物质的量变化的曲线,实线表示Al3+,虚线表示AlO2-,其中正确的是
- 若集合M=,P={y|y=},那么M∩P=.
- 若函数是偶函数,则的递减区间是 ;



