八年级(初二)数学下学期下册试题
如图,已知正方形ABCD边长为1,E为AB边上一点,以点D为中心,将  按逆时针方向旋转得
按逆时针方向旋转得  ,连接EF,分別交BD,CD于点M,N.若
,连接EF,分別交BD,CD于点M,N.若  ,则
,则  .
.
 按逆时针方向旋转得
按逆时针方向旋转得  ,连接EF,分別交BD,CD于点M,N.若
,连接EF,分別交BD,CD于点M,N.若  ,则
,则  .
.

在直角坐标系中,点P(2,-3)到原点的距离是.
6月26日是“国际禁毒日”,某中学组织七,八年级全体学生开展了“禁毒知识”网上竞赛活动,为了了解竞赛情况,从这两个年级分别随机抽取了10名学生的成绩(满分为100分),将收集到的数据整理分析并绘制成两个不完整的统计表:
|
分数 人数 年级 |
80 |
85 |
90 |
95 |
100 |
平均数 |
中位数 |
众数 |
方差 |
||
|
七年级 |
2 |
2 |
3 |
2 |
1 |
七年级 |
89 |
|
90 |
39 |
|
|
八年级 |
1 |
2 |
4 |
|
1 |
八年级 |
|
90 |
|
30 |
请根据以上信息,解答下列问题:
-
(1) 写出表格中
 ,
,  ,
,  ,
,  的值;
的值;
-
(2) 通过数据分析,你认为哪个年级的学生成绩比较好?说明你的理由;
-
(3) 该校七、八年级学生共有600人,本次竞赛成绩不低于90分为“优秀”,估计这两个年级达到成绩“优秀”的学生共有多少人?
阅读下面材料
在数学课上,老师提出如下问题:
|
已知:如图,△ABC及AC边的中点O。 求作:平行四边形ABCD。 |
小敏的作法如下:
| ①连接BO并延长,在延长线上截取OD=BO; ②连接DA、DC 所以四边形ABCD就是所求作的平行四边形。 |
老师说:“小敏的作法正确。”
请回答:小敏的作法正确的理由是。
化简:  = ,
= ,  = .
= .
 = ,
= ,  = .
= .
如图,在矩形ABCD中,E在AD上, ,交CD于F,连结BF,则图中与△ABE 一定相似的三角形是( )
,交CD于F,连结BF,则图中与△ABE 一定相似的三角形是( )
A . △EFB
B . △DEF
C . △CFB
D . △EFB与△DEF
平行四边形的对角线长度分别为6cm和10cm,则一组对边的长可能是( )
A . 2cm
B . 4cm
C . 8cm
D . 16cm
如图所示,直线l1 , l2相交于点A,则点A的坐标为

在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为

在平面直角坐标系中,点P(-  ,-1)到原点的距离是多少?
,-1)到原点的距离是多少?
 ,-1)到原点的距离是多少?
,-1)到原点的距离是多少?
若四边形ABCD的顶点坐标分别是A(-2,0),B(0,1),C(2,0),D(0,-1),则四边形ABCD是( )
A . 矩形
B . 菱形
C . 正方形
D . 非平行四边形
化简:  ﹣
﹣  =.
=.
 ﹣
﹣  =.
=.
如图,在每个小正方形的边长为1的网格中,  的顶点A , B在格点上,C是小正方形边的中点.
的顶点A , B在格点上,C是小正方形边的中点.
 的顶点A , B在格点上,C是小正方形边的中点.
的顶点A , B在格点上,C是小正方形边的中点. 
-
(1)
 的长等于;
的长等于;
-
(2) M是线段
 与网格线的交点,P是
与网格线的交点,P是  外接圆上的动点,点N在线段
外接圆上的动点,点N在线段  上,且满足
上,且满足  .当
.当  取得最大值时,请在如图所示的网格中,用无刻度的直尺,画出点P , 并简要说明点P的位置是如何找到的(不要求证明).
取得最大值时,请在如图所示的网格中,用无刻度的直尺,画出点P , 并简要说明点P的位置是如何找到的(不要求证明).
四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=4  EF,则正方形ABCD的面积为
EF,则正方形ABCD的面积为
 EF,则正方形ABCD的面积为
EF,则正方形ABCD的面积为

化简  =.
=.
 =.
=.
如图,将平行四边形ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,有以下四个结论①MN∥BC;②MN=AM;③四边形MNCB是矩形;④四边形MADN是菱形,以上结论中,你认为正确的有(填序号).


计算:
-
(1)
 ;
;
-
(2)
 .
.
如图,在矩形  中,两条对角线
中,两条对角线 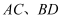 相交于点O,若
相交于点O,若  ,则
,则  .
.
 中,两条对角线
中,两条对角线 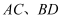 相交于点O,若
相交于点O,若  ,则
,则  .
. 
探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图像特征,概括函数性质的过程.结合已有的学习经验,请画出函数 的图象并探究该函数的性质.
的图象并探究该函数的性质.
 的图象并探究该函数的性质.
的图象并探究该函数的性质.
|
x |
… |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
… |
|
|
… |
|
a |
|
|
b |
|
|
|
|
… |
|
|
c |
d |
e |
f |
g |

-
(1) 列表,写出表中a,b的值:a= ▲ , b= ▲ ;描点、连线,在所给的平面直角坐标系中画出该函数的图象.
-
(2) 观察函数图象,判断下列关于函数性质的结论是否正确,在下面横线上填入“序号”或填入“无”,正确的是,错误的是.
①函数
 的图象关于y轴对称;
的图象关于y轴对称;②当
 时,函数
时,函数 有最小值,最小值为
有最小值,最小值为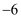 ;
;③在自变量的取值范围内函数y的值随自变量x的增大而减小.
-
(3) 已知二次函数
 , 请你写出表中c,d,e,f,g的值:c= ▲ , d= ▲ , e= ▲ , f= ▲ , g= ▲ , 并在所给的同一坐标系中画出函数
, 请你写出表中c,d,e,f,g的值:c= ▲ , d= ▲ , e= ▲ , f= ▲ , g= ▲ , 并在所给的同一坐标系中画出函数 的图像,结合你所画的函数图象,直接写出不等式
的图像,结合你所画的函数图象,直接写出不等式 的解集.
的解集.
当k<0时,一次函数y=kx﹣k的图象不经过( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
最近更新
- 下列大肠杆菌某基因的碱基序列的变化,对其所控制合成的多肽的氨基酸序列影响最大的是(不考虑终止密码子)() A.
- When I went to watch the 16th Asian Games last month, I was
- (14分)下列为元素周期表中的一部分,用化学式或元素符号回答下列问题: 族 周期 ⅠA ⅡA Ⅲ
- 形成“一粥一饭,当思来处不易;半丝半缕,恒念物力维艰”观念的社会背景是 A、小农经济盛行
- 在“探究摩擦力大小与哪些因素有关”的实验中,同学们提出了以下几种猜想: A.与物体的重力大小有关 B.与物体运动的速
- 狗熊偷食蜂巢中的蜂蜜,狗熊的行为属于∶ ( )A. 防御行为
- (本小题满分14分) 已知数列的首项,,. (Ⅰ)求的通项公式; (Ⅱ)证明:对任意的,,; (Ⅲ)证明:.
- 如图所示,在垂直纸面向里的匀强磁场的边界上,有两个质量和电量均相同的正、负离子(不计重力),从O点以相同的速度先后射入磁
- 读“台湾岛轮廓图”,回答1~3题。1.造成台湾岛东西部城市密度差异最主要的区位因素是 A.气候 B.地形
- 豌豆植株上,一个豆荚中含三粒种子,下列有关说法正确的是( ) A.该豆荚是由三个子房发育而来的 B.形成该豆荚需要
- 在pH=13的无色溶液中,可以大量共存的一组离子是 ( )
- 在我国,公民可以通过多种方式和渠道实现政治参与。对下列政治参与方式判断正确的是 ①甲对政府工作提出批评建议,表明甲行使民
- 某电池厂旁的河流淤泥中的蠕虫对镉有抵抗力。清除出河底大部分含镉的沉积物后,经过9代繁衍,研究人员发现蠕虫重新对镉变得脆弱
- ......
- 某溶液中可能含有H+、Na+、NH4+、Mg2+、Fe3+、Al3+、SO42-、HCO3-等离子。当向该溶液中加入一定
- 观察下列图片 图1《告工人、士兵和 农民书》发布 图2《和平法令》 图3列宁接见农民请愿代表以上图片说明( ) A
- The students ______the classroom, so it’s tidy and clean now
- 我国历史上最早建立军队,制定刑法,设置监狱是在( ) A夏朝 B商朝
- 宋代人口有1亿,耕地面积5.6亿亩;鸦片战争前,清代人口达到4亿,耕地只有11~12亿亩。相对于宋代,清代养活这么多人口
- 如图所示,在坐标原点O处,能向四周均匀发射速度大小相等、方向都平行于纸面的带正电粒子。在O点右侧有一半径为R的圆形薄板,













