八年级(初二)数学下学期下册试题
下列二次根式中,与  是同类二次根式的是( )
是同类二次根式的是( )
 是同类二次根式的是( )
是同类二次根式的是( )
A . 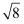 B .
B .  C .
C . 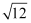 D .
D . 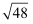
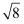 B .
B .  C .
C . 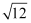 D .
D . 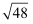
函数  中,自变量x的取值范围是.
中,自变量x的取值范围是.
 中,自变量x的取值范围是.
中,自变量x的取值范围是.
(﹣  )2的值为( )
)2的值为( )
 )2的值为( )
)2的值为( )
A . a
B . ﹣a
C . 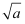 D . ﹣
D . ﹣ 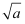
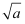 D . ﹣
D . ﹣ 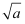
如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上. 对角线EG、FP相交于点O.

-
(1) 若AP=3,求AE的长;
-
(2) 连接AC,判断点O是否在AC上,并说明理由;
-
(3) 在点P从点A到点B的运动过程中,正方形PEFG也随之运动,求DE的最小值.
已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.

-
(1) 求证:EF与GH互相平分;
-
(2) 当四边形ABCD的边满足条件时,EF⊥GH.(不必证明)
要使式子  有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A . x>0
B . x≥﹣3
C . x≥3
D . x≤3
直角三角形的斜边长是5,一直角边是3,则此三角形的周长是.
已知 的面积为16,点D,E分别为AB,AC边上的中点,则四边形DBCE的面积为( )
的面积为16,点D,E分别为AB,AC边上的中点,则四边形DBCE的面积为( )
 的面积为16,点D,E分别为AB,AC边上的中点,则四边形DBCE的面积为( )
的面积为16,点D,E分别为AB,AC边上的中点,则四边形DBCE的面积为( )
A . 12
B . 10
C . 9
D . 8
甲、乙、丙、丁四人各进行10次射击测试,它们的平均成绩相同,方差分别是 ,
,  ,
,  ,
,  , 则射击成绩比较稳定的是( )
, 则射击成绩比较稳定的是( )
 ,
,  ,
,  ,
,  , 则射击成绩比较稳定的是( )
, 则射击成绩比较稳定的是( )
A . 甲
B . 乙
C . 丙
D . 丁
如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点中,离原点最近的是( )

A . 超市
B . 医院
C . 体育场
D . 学校
综合与探究
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣3,0)、B两点,与y轴相交于点  .当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC , BC .
.当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC , BC .

-
(1) 求抛物线的解析式;
-
(2) 判断△ABC的形状,并说明理由;
-
(3) 若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动,当运动时间为t秒时,连接MN , 将△BMN沿MN翻折,B点恰好落在AC边上的P处,则t的值为,点P的坐标为;
-
(4) 抛物线对称轴上是否存在一点F , 使得△ACF是以AC为直角边的直角三角形?若不存在,请说明理由;若存在,请直接写出点F的坐标.
小明某学期的数学平时成绩70分,期中考试80分,期末考试85分,若计算学期总评成绩的方法如下:平时:期中:期末=3:3:4,则小明总评成绩是分.
式子 化简的结果是 .
化简的结果是 .
 化简的结果是 .
化简的结果是 .
直线  经过点
经过点  、
、 
 经过点
经过点  、
、 

-
(1) 求直线
 的解析式;
的解析式;
-
(2) 若点C在x轴上,且
 求出点C坐标.
求出点C坐标.
下列说法不正确的是( )
A . 在选举中,人们通常最关心的数据是众数
B . 数据3,5,4,1,﹣2的中位数是3
C . 一组数据1,1,0,2,4的平均数为2
D . 甲、乙两人数学成绩的平均分都是95,方差分别是2.5和10.5,要选择一人参加数学竞赛,选甲比较稳定
如图,在▱ABCD中,对角线AC、BD交于点O,AC⊥CD,若AC=8,CD=3,则BD的长是( )

A . 8
B . 10
C . 12
D . 14
下列说法正确的是( )
A . 一个游戏中奖的概率是 , 则做100次这样的游戏一定会中奖
B . 为了了解全国中学生的心理健康状况,应采用普查的方式
C . 一组数据0,1,2,1,1的众数和中位数都是1
D . 若甲组数据的方差S2=0.2,乙组数据的方差S2=0.5,则乙组数据比甲组数据稳定
, 则做100次这样的游戏一定会中奖
B . 为了了解全国中学生的心理健康状况,应采用普查的方式
C . 一组数据0,1,2,1,1的众数和中位数都是1
D . 若甲组数据的方差S2=0.2,乙组数据的方差S2=0.5,则乙组数据比甲组数据稳定
 , 则做100次这样的游戏一定会中奖
B . 为了了解全国中学生的心理健康状况,应采用普查的方式
C . 一组数据0,1,2,1,1的众数和中位数都是1
D . 若甲组数据的方差S2=0.2,乙组数据的方差S2=0.5,则乙组数据比甲组数据稳定
, 则做100次这样的游戏一定会中奖
B . 为了了解全国中学生的心理健康状况,应采用普查的方式
C . 一组数据0,1,2,1,1的众数和中位数都是1
D . 若甲组数据的方差S2=0.2,乙组数据的方差S2=0.5,则乙组数据比甲组数据稳定
如图,菱形ABCD的对角线相交于点O,若AC=8,BD=6,则菱形ABCD的周长是 ( )

A . 32
B . 24
C . 20
D . 40
a,b,c 是△ABC的∠A,∠B,∠C的对边,且a:b:c=1:  :
:  ,则cosB的值为 ( )
,则cosB的值为 ( )
 :
:  ,则cosB的值为 ( )
,则cosB的值为 ( )
A .  B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2  ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为
 ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为
最近更新
- 在南方谈话中指出“社会主义要赢得与资本主义相比较的优势,就必须大胆吸收和借鉴人类社会创造的一切文明成果。”在这一思想指导
- 右图为某细胞结构示意图,下列选项中的变化都会在该细胞中发生的是()A.氨基酸→胰岛素;ATP→ADP+Pi B.氨基酸→
- -3+(—1)÷+(—5)
- 如图所示,将带电棒移近两个不带电的导体球,两个导体球开始时互相接触且对地绝缘,下述几种方法中能使两球都带电的是
- 写出一个过点(0,3),且函数值y随自变量x的增大而减小的一次函数关系式: .(填上一个答案即可)
- 图11为“海洋等温线分布示意图”,其中表示南半球寒流的是
- 现实生活中不少人崇拜货币,相信货币拥有神奇的魔力。从根本上说,货币的神奇之处在于 ①其本质是一般等价物
- 下列各组词语中,有错别字的一组是( ) A.恐怖 步履 名列前茅 冉冉升起 B.踉跄
- (2009年4月上海市黄浦区高考模拟31题)文字的诞生是人类进入文明社会的重要标志之一。阅读下列材料,回答问题。(7分)
- “入世”十多年来,我国实施“走出去”战略,极大地提高了开放型经济水平。我国要增强“走出去”的能力,需要 ①创新对外投资
- 根据人口发展状况,我国应 A.提高人口自然增长率 B.加大自然资源开发力度 C.完善社会养老保障体系 D.大力提高农
- 读“波罗的海含量变化图”,分析完成下列问题。(1)波罗的海是世界盐度_________的海区。其主要原因是______
- 如图甲是某种特异性免疫的大致过程,图乙是初次免疫和二次免疫的相关情况变化曲线。下列关于它们的叙述中,正确的是
- 将0.1 mol·L-1醋酸溶液加水稀释,下列说法正确的是( ) A.溶液中c(H+)和c(OH-)都减小
- 秦岭—淮河一线大致同哪些界线相一致( )①1月0℃等温线②400毫米年等降水量线③800毫米年等降水量线④热带与亚热带的
- 中国人民银行宣布,自2015年3月1日起下调金融机构人民币存贷款基准利率,这是央行自去年11月之后再次降息。央行再次降息
- (本小题满分12分) 已知数列满足条件:, (1)求的值, (2)求数列的通项公式。
- 语言是一种味道,人们依靠它传情达意;语言更是一面镜子,人们从中可以看到时代的身影。问候语的变迁体现的哲学道理是A.社会意
- 下列有关物质性质与用途的说法,错误的是() A.石墨有滑腻感,可用来作电极 B.焦炭有还原性,可用于冶金工业 C.活性
- 1979年元旦,全国人大常委会在《告台湾同胞书》中指出:“在解决统一问题时,尊重台湾的现状和台湾各界人士的意见,采取合情



