八年级(初二)数学下学期下册试题
下列式子没有意义的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算:  .
.
 .
.
在  中,
中,  ,
,  ,
,  .
.
 中,
中,  ,
,  ,
,  .
. 
-
(1) 如图1,求点C到边
 的距离;
的距离;
-
(2) 点M是
 上一动点.
上一动点. ①如图2.过点M作
 交
交  于点N,当
于点N,当  时,求
时,求  的长;
的长;②如图3,连接
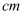 ,当
,当  为何值时,
为何值时,  为等腰三角形?
为等腰三角形?
在一个四边形ABCD中依次连接各边的中点得到的四边形是矩形,则对角线AC与BD需要满足的条件是( )
A . 垂直
B . 相等
C . 垂直且相等
D . 不再需要条件
使函数y=  有意义的自变量x的取值范围是。
有意义的自变量x的取值范围是。
 有意义的自变量x的取值范围是。
有意义的自变量x的取值范围是。
甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示

-
(1) 求甲车从A地到达B地的行驶时间;
-
(2) 求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
-
(3) 求乙车到达A地时甲车距A地的路程.
如图,在 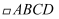 中,点E在AB上,
中,点E在AB上,  ,ED和AC相交于点F,过点F作
,ED和AC相交于点F,过点F作  ,交AD于点G.
,交AD于点G.
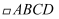 中,点E在AB上,
中,点E在AB上,  ,ED和AC相交于点F,过点F作
,ED和AC相交于点F,过点F作  ,交AD于点G.
,交AD于点G. 
-
(1) 求
 的值.
的值.
-
(2) 若
 ,
, ①求证:
 .
.②求证:
 .
.
已知一次函数y=kx+b的图像经过点(-2,4),且与正比例函数y=2x的图像平行.
-
(1) 求一次函数y=kx+b的解析式;
-
(2) 求一次函数y=kx+b的图像与坐标轴所围成的三角形的面积;
-
(3) 若A(a,y1),B(a+b,y2)为一次函数y=kx+b的图像上两个点,试比较y1与y2的大小.
如图,直线y=2x+3与反比例函数y  的图像相交于点B(a , 5),且与x轴相交于点A
的图像相交于点B(a , 5),且与x轴相交于点A

-
(1) 求反比例函数的表达式.
-
(2) 若P为反比例函数图象上一点,且△AOP的面积是△AOB的面积的
 ,请求出点P的坐标.
,请求出点P的坐标.
直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图那样折叠,使点A与点B重合,则折痕BE的长是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A . 48
B . 36
C . 24
D . 18
如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数y=  在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为( )
在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为( )
 在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为( )
在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为( )
A . 12
B . 10
C . 8
D . 6
某学校要招聘一名教师,分笔试和面试两次考试,笔试、面试和最后得分的满分均为100分,竞聘教师的最后得分按笔试成绩:面试成绩=3:2的比例计算.在这次招聘考试中,某竞聘教师的笔试成绩为90分,面试成绩为80分,则该竞聘教师的最后成绩是( )
A . 43分
B . 85分
C . 86分
D . 170分
计算 ﹣
﹣ =( )
=( )
 ﹣
﹣ =( )
=( )
A . 6
B . 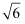 C . 2
D .
C . 2
D . 
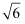 C . 2
D .
C . 2
D . 
若点A(1,y1)和点B(2,y2)都在一次函数y=﹣x+2的图象上,则y1y2(选择“>”、“<”、=”填空).
等式  成立的条件是( ).
成立的条件是( ).
A . a、b同号
B .  C .
C .  D .
D . 
如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是
A . S四边形ABCD=S四边形ECDF
B . S四边形ABCD<S四边形ECDF
C . S四边形ABCD=S四边形ECDF+1
D . S四边形ABCD=S四边形ECDF+2
如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(-1,0),(5,0),(0,2)
(1)求过A、B、C三点的抛物线解析式.
(2)若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P运动的时间为t秒,(0≤t≤6)设△PBF的面积为S.
①求S与t的函数关系式.
②当t是多少时,△PBF的面积最大,最大面积是多少?
(3)点P在移动的过程中,△PBF能否成为直角三角形?若能,直接写出点F的坐标;若不能,请说明理由.

如图, 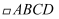 的对角线
的对角线  与
与  相交于点O,且
相交于点O,且  .若E是
.若E是  边的中点,
边的中点,  ,
,  ,则
,则  的长为( )
的长为( )
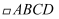 的对角线
的对角线  与
与  相交于点O,且
相交于点O,且  .若E是
.若E是  边的中点,
边的中点,  ,
,  ,则
,则  的长为( )
的长为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某校260名学生参加植树活动要求每人植4~7棵活动结束后随机抽查了20名学生每人的植树量,并分成四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形统计图(如图1所示)和条形统计图(如图2所示),经确认扇形统计图是正确的,而条形统计图尚有一处不符合题意.

回答下列问题:
-
(1) 写出条形统计图中存在的错误,并说明理由;
-
(2) 直接写出这20名同学每人植树量的中位数;
-
(3) 在求这20名同学每人植树量的平均数时,小宇是这样分析的:
第一步:求平均数的公式是
 ;
;第二步:在该问题中,
 ;
;第三步:
 (棵).
(棵).小宇的分析存在错误,请帮助他求出正确的平均数,并估计这260名学生共植树多少棵?
最近更新
- 在铁路与公路的交叉路口,安装有自动控制的
- 图1-2-8是某校园的平面示意图.假设某同学在教
- 把0.1molNaCl固体溶于水,配成1L 溶液,溶液中Na
- .据中国海关统计,从19世纪70年代到80年代末
- 在俄罗斯、美国、加拿大均有大面积分布的自
- 已知R2+有b个中子,核外有a个电子,表示R原
- 很多动物为了适应自身生存的环境,进化出了
- “蹦极跳”是一种能获得强烈失重、超重感觉
- 在△ABC中,tanAsin2B=tanBsin2A,那么△ABC一定是( �
- —I am going to Australia next week. —The radio says
- 阅读下面的文字,完成各题。 听油菜花开的
- 近年来,世界范围内农田生态系统有两个突出
- 在pH=12的无色溶液中,下列离子能大量共存的
- sin2(π+α)-cos(π+α)·cos(-α)+1=________.
- 焰色反应每次实验都要先用某一试剂洗净铂丝
- 如图K38-13所示,在铅板A上放一个放射源C,
- 关于Na2CO3和NaHCO3性质的说法不正确的是 A.热
- 关于氧化还原反应的下列说法中正确的是(
- 根据首字母完成句子 1. As we know, Fei Junlong and
- 观察是生活的必须,思考的前提。生活中你肯



