八年级(初二)数学下学期下册试题
如图,在 中,
中, . 将
. 将 折叠,使点B恰好落在边
折叠,使点B恰好落在边 上,与点
上,与点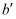 重合,
重合, 为折痕,则
为折痕,则 的周长为.
的周长为.
 中,
中, . 将
. 将 折叠,使点B恰好落在边
折叠,使点B恰好落在边 上,与点
上,与点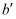 重合,
重合, 为折痕,则
为折痕,则 的周长为.
的周长为.
已知正比例函数y=(2k-3)x的图象过点(-3,5),则k的值为 ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,矩形ABCD中,AB=4,AD=9,点M在BC上,且BM:MC=1:2,DE⊥AM于点E,求DE的长为

如图,在□ABCD中,∠BCD的平分线交直线AD于点F,∠BAD的平分线交DC延长线于E,交线段BC于H点

-
(1) 证明:四边形AHCF是平行四边形;
-
(2) 证明:AF=EC;
-
(3) 若∠BAD=90°,G为CF的中点(如右图),判断△BEG的形状,并证明;
-
(4) 在(3)的条件上,若已知AB=6,BC=7,试求△BEG的面积.
如图,在平行四边形  中,
中,  ,若
,若  ,则
,则 
 .
.
 中,
中,  ,若
,若  ,则
,则 
 .
. 
如图,在长方形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )

A . 4
B . 5
C . 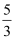 D .
D . 
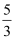 D .
D . 
某中学为了解学生参加户外活动的情况,随机调查了该校部分学生每周参加户外活动的时间,并用得到的数据绘制了如下统计图.

请根据以上信息,解答下列问题:
-
(1) 这次调查的学生共 ▲ 人,并补全条形统计图;
-
(2) 求本次调查获取的样本数据的平均数、众数和中位数;
-
(3) 若该校共有1500名学生,估计该校参加户外活动时间超过3小时的学生人数.
综合与探究:在平面直角坐标系  中,已知抛物线
中,已知抛物线  与
与  轴交于
轴交于  ,
,  两点(点
两点(点  在点
在点  的右侧),与
的右侧),与  轴交于点
轴交于点  ,它的对称轴与
,它的对称轴与  轴交于点
轴交于点  ,直线
,直线  经过
经过  ,
,  两点,连接
两点,连接  .
.
 中,已知抛物线
中,已知抛物线  与
与  轴交于
轴交于  ,
,  两点(点
两点(点  在点
在点  的右侧),与
的右侧),与  轴交于点
轴交于点  ,它的对称轴与
,它的对称轴与  轴交于点
轴交于点  ,直线
,直线  经过
经过  ,
,  两点,连接
两点,连接  .
. 
-
(1) 求
 ,
,  两点的坐标及直线
两点的坐标及直线  的函数表达式;
的函数表达式;
-
(2) 探索直线
 上是否存在点
上是否存在点  ,使
,使  为直角三角形,若存在,求出点
为直角三角形,若存在,求出点  的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
-
(3) 若点
 是直线
是直线  上的一个动点,试探究在抛物线上是否存在点
上的一个动点,试探究在抛物线上是否存在点  :
: ①使以点
 ,
,  ,
,  ,
,  为顶点的四边形为菱形,若存在,请直接写出点
为顶点的四边形为菱形,若存在,请直接写出点  的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;②使以点
 ,
,  ,
,  ,
,  为顶点的四边形为矩形,若存在,请直接写出点
为顶点的四边形为矩形,若存在,请直接写出点  的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF。下列结论正确的是( )

A . CE=  B . EF=
B . EF=  C . cos∠CEP=
C . cos∠CEP=  D . HF2=EF·CF
D . HF2=EF·CF
 B . EF=
B . EF=  C . cos∠CEP=
C . cos∠CEP=  D . HF2=EF·CF
D . HF2=EF·CF
如图,直线 与直线
与直线 相交于点A(m,4),且与x轴相交于点B,与y轴交于点C.
相交于点A(m,4),且与x轴相交于点B,与y轴交于点C.
 与直线
与直线 相交于点A(m,4),且与x轴相交于点B,与y轴交于点C.
相交于点A(m,4),且与x轴相交于点B,与y轴交于点C.
-
(1) 求a和m的值;
-
(2) 求△AOC的面积.
如图,在Rt△ABC中,∠ACB=90°,D为边AC上一点,且BC=3CD,BD=10。

-
(1) 求CD的长;
-
(2) 若AB=5
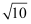 ,求AD的长。
,求AD的长。
如图,平行四边形ABCD的对角线AC、BD相交于点O , 若AC+BD=24厘米,△OAB的周长是18厘米,则AB的长为( )

A . 6厘米
B . 12厘米
C . 5厘米
D . 9厘米
在化简 时,甲、乙两位同学的解答如下:
时,甲、乙两位同学的解答如下:
 时,甲、乙两位同学的解答如下:
时,甲、乙两位同学的解答如下:甲: ;
;
乙: .
.
这两位同学的解法,你认为( )
A . 两人解法都对
B . 甲错乙对
C . 甲对乙错
D . 两人都错
如图,AB是⊙O的直径,⊙O的半径为5cm,弦AC的长为6cm,求弦BC的长.

在平面直角坐标系xOy中,  ABC三个顶点的坐标分别为A(0,2),B(2,0),C(5,3).
ABC三个顶点的坐标分别为A(0,2),B(2,0),C(5,3).
 ABC三个顶点的坐标分别为A(0,2),B(2,0),C(5,3).
ABC三个顶点的坐标分别为A(0,2),B(2,0),C(5,3).
-
(1) 点C关于x轴对称的点C1的坐标为,点C关于y轴对称的点C2的坐标为.
-
(2) 试说明
 ABC是直角三角形.
ABC是直角三角形.
-
(3) 已知点P在x轴上,若
 ,求点P的坐标.
,求点P的坐标.
如图,菱形 中,
中, ,
,  坐标为
坐标为 , 再以
, 再以 为对称中心作菱形
为对称中心作菱形 , 再以
, 再以 为对称中心作菱形
为对称中心作菱形 , 按此规律继续作下去,得到菱形
, 按此规律继续作下去,得到菱形 , 则
, 则 的坐标为.
的坐标为.
 中,
中, ,
,  坐标为
坐标为 , 再以
, 再以 为对称中心作菱形
为对称中心作菱形 , 再以
, 再以 为对称中心作菱形
为对称中心作菱形 , 按此规律继续作下去,得到菱形
, 按此规律继续作下去,得到菱形 , 则
, 则 的坐标为.
的坐标为.
计算:
-
(1)

-
(2)

如图,已知一次函数  的图象与反比例函数
的图象与反比例函数  的图象交于点
的图象交于点  ,点
,点  .
.
 的图象与反比例函数
的图象与反比例函数  的图象交于点
的图象交于点  ,点
,点  .
. 
-
(1) 求反比例函数的表达式;
-
(2) 若一次函数图象与y轴交于点C , 点D为点C关于原点O的对称点,求
 的面积.
的面积.
如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( )

A . 8≤AB≤10
B . 8<AB≤10
C . 4≤AB≤5
D . 4<AB≤5
化简  的结果是( )
的结果是( )
 的结果是( )
的结果是( )
A . ﹣2
B . ±2
C . 2
D . 4
最近更新
- The heavy snow swept across manyparts of China, _________ m
- (12分)如图 (a)所示是某人设计的一种振动发电装置,它的结构是一个半径为r=0. 1 m的20匝线圈,线圈套在永久磁
- 某物体做直线运动的速度—时间图象如图所示,试根据图象回答下列问题: (1)物体在OA段做______运动,加速度是___
- 如图5所示,在薄皮铁桶内放些水,烧开后把开口堵住,再浇上冷水,发现皮桶变扁了,这个现象证明了 的存在。薄皮铁桶被压
- 5.甲、乙、丙、丁四地中风速最大的是 ( ) A.甲
- 2002年4月21日上午9时30分左右,武汉上空的太阳周围环绕一道“美丽的光环”,这是太阳的“日晕”现象.这种现象A.属
- 右图为小麦叶肉细胞中两种细胞器的模式图。下列叙述中,正确的是 A.两种细胞器以相同的方式增大膜面积,②③均具有光合色素
- 如图所示为函数y=Asin(ωx+φ)的图像上的一段,则这个函数的解析式为______________.
- 关于静摩擦力,下列说法正确的是() A.两个相对静止的物体之间一定有静摩擦力的作用 B.静摩擦力一定是阻力 C.受静摩擦
- 北魏孝文帝迁都洛阳后,龙门石窟佛像造型逐渐呈现汉化的风格。这反映了 ( )A.佛教的传入
- 阅读下面的材料,根据要求作文。 一只蜗牛,很想做成一番惊天动地的大事业。开始它想东游泰山,一直爬到山顶,可一计算,要实现
- 下列各句中,加点的成语使用恰当的一句是 ( )
- 已知点是圆上的动点. (1)求的取值范围;(2)若恒成立,求实数的取值范围.
- 长汀县古城镇每到农历二月十五要庆贺花的生日,即过“花朝节”。 当天,古城集镇人头攒动,热闹非凡,家家祭花神,祈求花神降福
- 列方程解应用题: 在一次同学聚会中,每两名同学之间都互送了一件礼物,所有同学共送了90件礼物,共有多少名同
- 甲醛、乙酸和丙醛组成的混合物中,氧元素的质量分数是37%,则碳元素的质量分数为 A.27%
- 2008年11月22日,在亚太经合组织第十六次领导人非正式会议上的讲话指出,我们主张,面对新的复杂局面,面对全球金融危机
- 2008年9月25日21时10分,神舟七号飞船在酒泉卫星发射中心成功升空。之后,航天员翟志刚成功出舱,实现中国历史上第一
- The island is ____ attractive in spring and autumn because o
- 2009年,云南省全面推进兴边富民、人口较少民族地区和特困民族地区扶持发展、民族特色村寨保护与发展等工程。各级政府共投入



