若点A(﹣3，y₁)和点B(1，y₂)都在如图所示的直线上，则y₁与y₂的大小关系为（    ）

已知一个平行四边形两邻边的长分别为10和6，那么它的周长为（  ）

如图1，正方形纸片ABCD边长为2，折叠∠B和∠D，使两个直角的顶点重合于对角线BD上的一点P，EF、GH分别是折痕（图2），设AE=x（0＜x＜2），给出下列判断：①x= 时，EF+AB＞AC；②六边形AEFCHG周长的值为定值；③六边形AEFCHG面积为定值，其中正确的是（   ）

如图，有一块边长为2 的正方形厚纸板ABCD，做成如图①所示的一套七巧板（点O为正方形纸板对角线的交点，点E，F分别为AD，CD的中点，CE∥BI，IH∥CD），将图①所示七巧板拼成如图②所示的“鱼形”，则“鱼尾”MN的长为（　　）

在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，则⊙O的面积是（　　）

如图，正方形ABCD中，AB=4，动点E从点A出发向点D运动，同时动点F从点D出发向点C运动，点E、F运动的速度相同，当它们到达各自终点时停止运动，运动过程中线段AF、BE相交于点P，M是线段BC上任意一点，则MD+MP的最小值为．

若三角形的三边长为下列各组数：①5，12，13；②11，12，15；③9，40，41；④15，20，25，则其中直角三角形有（　　）个

某青年排球队12名队员的年龄情况如下：

则12名队员的年龄（    ）

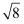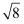计算:〡一 〡= ．

如图，已知四边形 中， 、 分别为 、 上的点， 、 分别为 、 的中点．当点 在 上从点 向点 移动而点 不动时，那么下列结论成立的是（   ）

计算（＋＋＋…＋） 

已知m＝ +1，n＝ ﹣1，则代数式m²+n²﹣3mn的值为.

在一次九年级学生视力检查中．随机检查了8个人的右眼视力，结果如下：4.0，4.2，4.5，4.0，4.4，4.5，4.0，4.8．则下列说法中正确的是（　　）.

如图，在□ABCD中，对角线AC，BD交于点O，∠BAC=90°，E为AB的中点，若AE=3，AO=4，则AD的长为（   ）

二元一次方程的图象如图所示，则这个二元一次方程为（　　）

如图，已知Rt△ABC中，∠ACB=90°，AC=6，BC=8.以AB为边作正方形ABEF，连CE，则△CBE的面积为

随着地铁和共享单车的发展，“地铁+单车”已成为很多市民出行的选择，李华从文化宫站出发，先乘坐地铁，准备在离家较近的A，B，C，D，E中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与文化宫距离为x（单位：千米），乘坐地铁的时间y₁（单位：分钟）是关于x的一次函数，其关系如下表：

地铁站	A	B	C	D	E
x（千米）	8	9	10	11.5	13
y1（分钟）	18	20	22	25	28

若5y+2与x－3成正比例，则y是x的（    ）

如图，在△ABC中，∠ACB＝90°，以它的三边为边分别向外作正方形，面积分别为S₁ ， S₂ ， S₃ ， 已知S₁＝5，S₂＝12，则S₃＝．

如图，在△ABC中，AB=5，BC=6，BC边上的中线AD=4．求AC的长．