七年级(初一)数学：上学期上册　　 下学期下册

七年级(初一)数学下学期下册试题

李大爷有一块长方形菜地，且菜地的长是宽的2倍。

（1）若菜地的面积为98m² ，求菜地的长与宽；
（2）若菜地的面积为90m² ，这块菜地的宽是多少？（用根号表示）你能告诉李大爷这块菜地的宽在哪两个整数之间吗？

①a²－4a+4，②a²+a+ $\text{[math]}$ ，③4a²－a+ $\text{[math]}$ ，④4a²+4a+1，以上各式中属于完全平方式的有（填序号）．

不等式组 $\text{[math]}$ 的所有整数解的和为．

计算：

（1） [a(a²b²-ab)-b(-a³b-a²)]÷a²b；
（2） $\text{[math]}$ .

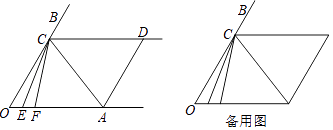
如图，已知射线CD∥OA，点E、点F是OA上的动点，CE平分∠OCF，且满足∠FCA=∠FAC．

（1）若∠O=∠ADC，判断AD与OB的位置关系，证明你的结论．
（2）若∠O=∠ADC=60°，求∠ACE的度数．
（3）在（2）的条件下左右平行移动AD，∠OEC和∠CAD存在怎样的数量关系？请直接写出结果（不需写证明过程）

解方程组 $\text{[math]}$ ．

在平面直角坐标系中，点(-2，-1)在第象限.

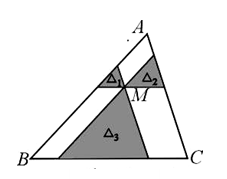
如图，点M是△ABC内一点，过点M分别作直线平行于△ABC的各边，所形成的三个小三角形△₁、△₂、△₃（图中阴影部分）的面积分别是4，9和49．则△ABC的面积是．

“a的一半与b的差不大于 $\text{[math]}$ ”用不等式表示为．

已知一个正数的平方根是2a+1和a-13，

（1）求这个正数；
（2）求 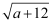$\text{[math]}$ 的平方根

不等式（a﹣b）x＜a﹣b的解集是x＞1，则a、b的大小关系是：ab．

对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M， N间的“邻近距离”，记为d（图形M，图形N）.已知点A（﹣2，﹣2），B（3，﹣2），C（3，3），D（﹣2，3）.

（1） d（点O，线段AB）＝；
（2）若点G在 x 轴上，且 d（点G，线段AB）＞2，直接写出点G的横坐标a的取值范围；
（3）依次连接 A，B，C，D 四点，得到正方形 ABCD（不含图形内部），记为图形M，点E（t，0），点 F（0， $\text{[math]}$ ﹣t）均不与点O重合，线段EO，OF组成的图形记为图形N，若1＜d（图形M，图形 N）＜2，求出t的取值范围.

在平面直角坐标系中，已知点A（﹣4，﹣1）和B（﹣1，4），平移线段AB得到线段A₁B₁ ，使平移后点A₁的坐标为（2，2），则平移后点B₁坐标是（）

A . （﹣3，1） B . （﹣3，7） C . （1，1） D . （5，7）

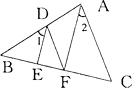
如图，已知AF平分∠BAC，DE平分∠BDF，且∠1=∠2，能判定DF∥AC吗？请说明理由？

建设中的大外环路是我市的一项重点民生工程.某工程公司承建的一段路基工程的施工土方量为120万立方，原计划由公司的甲、乙两个工程队从公路的两端同时相向施工150天完成.由于特殊情况需要，公司抽调甲队外援施工，由乙队先单独施工40天后甲队返回，两队又共同施工了110天，这时甲乙两队共完成土方量103.2万立方.

（1）问甲、乙两队原计划平均每天的施工土方量分别为多少万立方？
（2）在抽调甲队外援施工的情况下，为了保证150天完成任务，公司为乙队新购进了一批机械来提高效率，那么乙队平均每天的施工土方量至少要比原来提高多少万立方才能保证按时完成任务？

某中学为了解本校学生对球类运动的爱好情况，采用抽样的方法，从足球、篮球、排球、其它等四个方面调查了若干名学生，并绘制成“折线统计图”与“扇形统计图”．请你根据图中提供的部分信息解答下列问题：

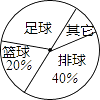
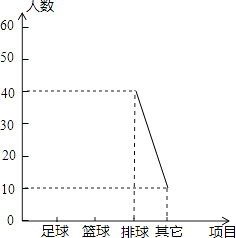
（1）在这次调查活动中，一共调查了名学生；
（2） “足球”所在扇形的圆心角是度；
（3）补全折线统计图．

下列调查中，适宜采用全面调查（普查）方式的是（）

A . 调查市场上老酸奶的质量情况 B . 调查马龙县中学生每周体育锻炼的时间 C . 调查某品牌圆珠笔的使用寿命 D . 调查乘坐飞机的旅客是否携带了危禁物品

（1）探究：如图①，DE∥BC，EF∥AB，若∠ABC＝50°，求∠DEF的度数．

请将下面的解答过程补充完整，并填空．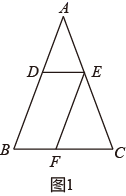
解：因为DE∥BC，

所以∠DEF＝                        ▲                  （             ▲                        ）．

因为EF∥AB，

所以                   ▲                  ＝∠ABC（                   ▲                  ）．

所以∠DEF＝∠ABC（等量代换）．

因为∠ABC＝50°，

所以∠DEF＝                  ▲                   ．
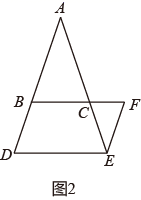
（2）
应用：如图②，DE∥BC，EF∥AB，若∠ABC＝65°，求∠DEF的度数．

已知m= (- 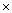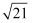$\text{[math]}$ ) $\text{[math]}$ (- $\text{[math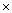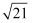]}$ )，则有（　　）

A . 2＜m＜3 B . 3＜m＜4 C . ﹣3＜m＜﹣2 D . ﹣4＜m＜﹣3

若|x-2|+|3x-6y|+（3y+z）²=0，则x+y+z的值为.

七年级(初一)数学： 上学期上册 下学期下册

七年级(初一)数学下学期下册试题

七年级(初一)数学：上学期上册　　下学期下册