在10件产品中，有3件一等品，4件二等品，3件三等品．从这10件产品中任取3件，求：
(1)取出的3件产品中一等品件数X的分布列和数学期望；
(2)取出的3件产品中一等品件数多于二等品件数的概率．
 

黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：

则第n个图案中有白色地面砖­­­_________________块.

中，若，，，则的面积为（    ）

A．         B．         C．1         D．

直线 （ 为参数）被曲线 所截的弦长_____

函数的导数是（   ）

A.     B.    C .    D.

已知命题p：函数的最小正周期为2π；命题q：函数的图象关于原点中心对称，则下列命题是真命题的是(　　)

A．p∧q      B．()∧()   C．p∨q    D．p∨()

某市纺织工人的月工资（元）依劳动生产率（千元）变化的回归方程为y=50+80x，则下列说法中正确的是（  ）

A．劳动生产率为1000元时，月工资为130元 

 B．劳动生产率提高1000元时，月工资提高约为130元

C．劳动生产率提高1000元时，月工资提高约为80元  

D．月工资为210元时，劳动生产率为2000元

函数有（    ）

A．极大值5，极小值－27；            B．极大值5，极小值－11；    

C ．极小值－27，无极大值；          D．极大值5，无极小值；

过圆外一点，作这个圆的两条切线、，切点分别是、，则直线的方程为______________________.

若集合A={x|x²+5x+4＜0}，集合B={x|x＜﹣2}，则A∩（∁_RB）等于（　　）

A．（﹣2，﹣1）  B．[﹣2，4）    C．[﹣2，﹣1）  D．

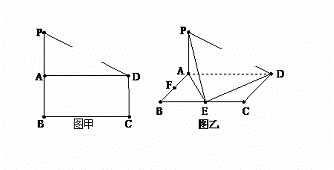
如图甲，在直角梯形PBCD中，PB∥CD， CD⊥BC，BC＝PB＝2CD，A是PB的中点．

现沿AD把平面PAD折起，使得PA⊥AB（如图乙所示），E、F分别为BC、AB边的中点．

（1）求证：平面PAE⊥平面PDE；

（2）在PE上找一点Q，使得平面BDQ⊥平面ABCD．

（3）在PA上找一点G，使得FG∥平面PDE．

扇形中，，其中是的中点，是弧上的动点（含端点），若实数满足，则的取值范围是（   ）

A．   B．   C．  D．

如图，在直四棱柱ABCD－A₁B₁C₁D₁中，底面ABCD为等腰梯形，AB∥CD，AB＝4，

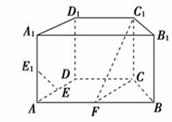BC＝CD＝2，AA₁＝2，E，E₁分别是棱AD，AA₁的中点．

（1）设F是棱AB的中点，证明：直线EE₁∥平面FCC₁；

（2）证明：平面D₁AC⊥平面BB₁C₁C；

（3）求点D到平面D₁AC的距离．

如图，椭圆的上顶点、左顶点、左焦点分别为B、A、F，中心为O，其离心率为，则

A．     B．     C．     D．

已知数列满足：，，，

（1）求证：数列为等差数列；

（2）求数列的通项公式；

（3）设，求数列的前项和.

78与36的最大公约数是(   )

A. 24    B. 18    C. 12    D. 6

函数的图象恒过定点，若点在直线上，则的最小值为             .  

如图,在四棱锥中,平面,,且,点在上．

（Ⅰ）求证:;

（Ⅱ）若二面角的大小为,求与平面所成角的正弦值．

 对标有不同编号的16件正品和4件次品的产品进行检测，不放回地依次摸出2件．在第一次摸出次品的条件下，第二次也摸到次品的概率是(　　)

A．          B．         C．        D．

△ABC中，角A、B、C的对边分别为a、b、c．已知（a+c）²﹣b²=3ac

（1）求角B；（2）当b=6，sinC=2sinA时，求△ABC的面积．