初中 数学
我国民间流传着许多趣味算题,它们多以顺口溜的形式表达,其中《孙子算经》中记载了这样一个数学问题:一群老头去赶集,半路买了一堆梨,一人一个多一梨,一人两个少二梨,请问君子知道否,几个老头几个梨?
综合题。
-
(1) 计算:

-
(2) 计算:

如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=12cm,AD=15cm,BC=20cm,动点E从点A出发,在线段AD上以每秒1cm的速度向点D运动,动点F从点C出发,在线段CB上以每秒2cm的速度运动到B点返回,点E、F分别从点A、C同时出发,当点E运动到点D时,点F随之停止运动,设运动的时间为t(秒).


-
(1) 用含t的代数式表示DE,DE=;
-
(2) 若四边形EFCD是平行四边形,求此时t的值;
-
(3) 是否存在点F,使△FCD是等腰三角形?若存在,请直接写出所有满足要求的t的值;若不存在,请说明理由.
不等式组  的正整数解的个数是( )
的正整数解的个数是( )
 的正整数解的个数是( )
的正整数解的个数是( )
A . 1
B . 2
C . 3
D . 4
方程  的解是
的解是  ,则a的值是( )
,则a的值是( )
 的解是
的解是  ,则a的值是( )
,则a的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
三个关于 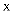 的方程:
的方程:  ,已知常数
,已知常数  ,若
,若  、
、  、
、  分别是按上顺序对应三个方程的正根,则下列判断正确的是( )
分别是按上顺序对应三个方程的正根,则下列判断正确的是( )
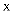 的方程:
的方程:  ,已知常数
,已知常数  ,若
,若  、
、  、
、  分别是按上顺序对应三个方程的正根,则下列判断正确的是( )
分别是按上顺序对应三个方程的正根,则下列判断正确的是( )
A .  B .
B .  C .
C .  D . 不能确定
D . 不能确定  的大小
的大小
 B .
B .  C .
C .  D . 不能确定
D . 不能确定  的大小
的大小
已知m<0,那么|  ﹣2m|值为.
﹣2m|值为.
 ﹣2m|值为.
﹣2m|值为.
如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是

如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.

-
(1) 当m=3时,求点A的坐标及BC的长;
-
(2) 当m>1时,连接CA,问m为何值时CA⊥CP?
-
(3) 过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.
从一个锐角  顶点出发在角的内部引一条射线,把
顶点出发在角的内部引一条射线,把  分成两个角,若其中一个角与
分成两个角,若其中一个角与  互余,则这条射线叫做锐角
互余,则这条射线叫做锐角  的余分线,这个角叫做锐角
的余分线,这个角叫做锐角  的余分角.
的余分角.
 顶点出发在角的内部引一条射线,把
顶点出发在角的内部引一条射线,把  分成两个角,若其中一个角与
分成两个角,若其中一个角与  互余,则这条射线叫做锐角
互余,则这条射线叫做锐角  的余分线,这个角叫做锐角
的余分线,这个角叫做锐角  的余分角.
的余分角.  例如:图①中,当
例如:图①中,当  时,
时,  与
与 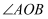 互余,那么
互余,那么 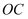 是
是 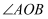 的余分线,
的余分线,  是
是 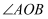 的余分角.
的余分角.
-
(1) 若
 ,
, 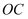 是它的余分线,则
是它的余分线,则  ;
;
-
(2) 如图②,
 是平角,
是平角,  是
是 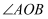 的余分角,
的余分角,  ,试说明
,试说明  .
.
-
(3) 如图③,在(2)的条件下,若
 是
是 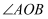 的平分线,
的平分线,  ,求
,求  度数.
度数.
正六边形内接于圆,它的边所对的圆周角是( )
A . 60°
B . 120°
C . 60°或120°
D . 30°或150°
若|a|=3,|b|=5,求a﹣b的值.
下列说法正确的是( )
A . 小红小学毕业时的照片和初中毕业时的照片相似
B . 商店新买来的一副三角板是相似的
C . 所有的课本都是相似的
D . 国旗的五角星都是相似的
一个圆锥和一个圆柱的高相等,若要使体积一样,圆锥底面积应是圆柱底面积的( )
A . 3倍
B .  C .
C .  倍
D .
倍
D . 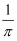
 C .
C .  倍
D .
倍
D . 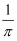
计算(3x3)2的结果是( )
A . 6x3
B . 9x6
C . 8x6
D . 8x5
-
(1) 计算:

-
(2) 求x的值:2x2﹣18=0
二次函数  的图象如图所示,根据图象回答:
的图象如图所示,根据图象回答:
 的图象如图所示,根据图象回答:
的图象如图所示,根据图象回答:

-
(1) 当
 时,写出自变量
时,写出自变量  的值.
的值.
-
(2) 写出
 随
随  的增大而减小的自变量
的增大而减小的自变量  的取值范围.
的取值范围.
-
(3) 若方程
 有两个不相等的实数根,求
有两个不相等的实数根,求  的取值范围(用含
的取值范围(用含  、
、  、
、  的代数式表示).
的代数式表示).
如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则  的值为.
的值为.
 的值为.
的值为.

若反比例函数y![]() 的图像经过第一、三象限,则 k的取值范围是 .
的图像经过第一、三象限,则 k的取值范围是 .
甲、乙两家商场以同样价格出售相同的商品,在同一促销期间两家商场都让利酬宾,让利方式如下:甲商场所有商品都按原价的8.5折出售,乙商场只对一次购物中超过200元后的价格部分按原价的7.5折出售.某顾客打算在促销期间到这两家商场中的一家去购物,设该顾客在一次购物中的购物金额的原件为x(x>0)元,让利后的购物金额为y元.
(1)分别就甲、乙两家商场写出y关于x的函数解析式;
(2)该顾客应如何选择这两家商场去购物会更省钱?并说明理由.
最近更新
- 向一定体积的0.1摩/升的醋酸溶液中加入等体积的蒸馏水后,则下列叙述正确的是() A.溶液的pH值变小 B.醋酸的电离
- 1892年,张弼士在烟台创办“张裕葡萄酿酒公司” 获得了巨大成功。在总结“张裕”创业史中他写道:“备历艰阻”、“掷无数之
- 如图所示,电源电压为12V且保持不变,灯泡L标有“6V,3W”的字样,滑动变阻器的最大阻值为50Ω,闭合开关S1,S2,
- (文)已知圆C:x2+y2-2x+4y=0,则通过原点且与圆C相切的直线方程为A.y=-2x
- 为了测出某种液体的密度ρ2;给你一只粗细均匀的圆柱形平底试管、一些小铁砂粒、两个烧杯,一个烧杯盛有水,一个盛有待测液体。
- 消费受很多因素的影响,其中主要是( ) A、商品性能、质量 B、居民收入水平和物价水
- 如图,小凳凳面为圆形,凳脚为三根细钢管.考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点与凳面圆
- (09年普陀区期末)(14分)如图(a)所示,两根足够长的水平平行金属导轨相距为L=0.5m,其右端通过导线连接阻值R=
- Dear Lucy,Thank you for your letter and yourinvitation. I re
- 宣传科学知识,介绍高新科技,揭露伪科学,是科学工作者的义务,下列各项中属于伪科学的是( )A.高温高压下将石墨制成
- 2014年距离第一次国共合作已90周年,近代史上国共曾两次合作,下列不属于国共合作的是( ) A.北伐战争
- 某含Na+的溶液中,可能还存在NH4+、Fe2+、Br﹣、CO32﹣、I﹣、SO42﹣六种离子中的一种或几种.进行以下实
- 下述做法符合低碳生活的是A.以煤等燃料作为主要生活燃料B.利用太阳能、风能和氢能等能源替代化石能源C.鼓励私人购买和使用
- (16分)、(1)有机化合物的结构简式可进一步简化,如:写出下列物质的分子式:① 分子式 用系统命名法对
- 下列思想主张吸收了阴阳五行学说的是
- 下列各组词语中加点字的读音与所给注音全都相同的一组是 A.龟guī 龟卜 龟鉴
- (08年天津南开区质检二文)(14分)已知某椭圆的焦点是,过点并垂直于x轴的直线与椭圆的一个交点为B,且。椭圆上不同的两
- 某遗传研究所成功培育出第一头携带人白蛋白基因的转基因牛,他们还研究出一种大大可提高基因表达水平的新方法,使转基因动物乳汁
- When the school bus arrived at the zoo, the busdoor ______ o
- 某未知溶液中已检验出含有离子Ca2+、NO3-,且pH=2。欲检验此溶液中是否大量存在以下6种离子:①ClO- ②NH4



