初中 数学

-
(1) 若已知∠AOB=120°,试求∠COD的度数;
-
(2) 若已知∠COD=18°,试求∠AOB的度数;
 D .
D . 
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 | a |
乒乓球 | 36 |
排球 | b |
足球 | 12 |

请根据以上图表信息解答下列问题:
-
(1) 频数分布表中的a=,b=;
-
(2) 在扇形统计图中,“排球”所在的扇形的圆心角为度;
-
(3) 全校有多少名学生选择参加乒乓球运动?
如图所示,河堤横断面迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),堤高BC=5m,则坡面AB的长度是( )
(坡比是坡面的铅直高度BC与水平宽度AC之比),堤高BC=5m,则坡面AB的长度是( )
 m
C . 15m
D . 5
m
C . 15m
D . 5 m
m

-
(1) A轮船沿哪个方向航行?请说明理由;
-
(2) 请求出此时A轮船到海岸线的距离.
已知:  ,求代数式
,求代数式  的值.
的值.
 的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
-
(1) 求这个二次函数的解析式;
-
(2) 点Q是线段AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与
 相似?若存在,求出点Q的坐标;若不存在,说明理由;
相似?若存在,求出点Q的坐标;若不存在,说明理由;
-
(3) 点M为抛物线上一动点,在x轴上是否存在点Q,使以A,C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
球的类别 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
-
(1) (
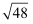 ﹣
﹣  )×
)× 
-
(2)
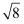 ﹣(
﹣(  ×
×  ﹣
﹣  )﹣
)﹣  ÷2.
÷2.
 ,得到△COD,则CD的长度是( )
,得到△COD,则CD的长度是( ) 
 D .
D . 
 并把解集在数轴上表示出来.
并把解集在数轴上表示出来. ![]()

-
(1) 如图1所示,在
 中,
中,  为
为  的中点,求证:
的中点,求证: 
甲说:不可能出现
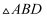
 ,所以此题无法解决;
,所以此题无法解决;乙说:根据倍长中线法,结合我们新学的平行四边形的性质和判定,我们可延长
 至点
至点  ,使得
,使得  ,连接
,连接  、
、 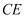 ,由于
,由于  ,所以可得四边形
,所以可得四边形  是平行四边形,请写出此处的依据(平行四边形判定的文字描述)
是平行四边形,请写出此处的依据(平行四边形判定的文字描述)所以
 ,
,  中,
中,  ,
,即

-
(2) 如图2,在
 中,
中,  为
为  的中点,
的中点, 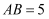 ,
,  ,
,  ,求
,求  的面积;
的面积;
-
(3) 如图3,在
 中,
中,  为
为  的中点,
的中点,  为
为  的中点,连接
的中点,连接  交
交  于
于  ,若
,若  .求证:
.求证:  .
.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3)。
(1)将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1,试在图上画出的图形Rt△A1B1C1的图形,
并写出点A1的坐标;
(2)将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2,试在图上画出Rt△A2B2C2的图形。
 |
二次函数的一般式为____________;若抛物线的顶点坐标为(h,k),则可设该抛物线的顶点式为____________;若抛物线与x轴交于(x 1 ,0)、(x 2 ,0),则可设该抛物线的两点式为____________.
- 化学与生产和生活密切相关。下列叙述错误的是( ) A.研制开发燃料电池汽车,可消除机动车尾气污染 B.大量燃烧化石燃料是
- 青藏高原纬度较低,却是我国夏季气温最低的地方,主要原因是( ) A.离海较远(位于西部) B.深居内陆
- 一矩形线圈位于一随时间t变化的匀强磁场内,设磁场方向垂直线圈所在的平面(纸面)向里为正,如图1所示,磁感应强度B随t的变
- Try on this red skirt; you will look great it.. A. on
- 图11为“某城市功能区分布示意图”,读图完成21~22题。21. 图中甲、乙、丙对应的功能区,正确的是 A. 商业区 工
- 【【.原创精品解析】历史卷·2015届四川省绵阳中学高三上学期第五次月考(201412)】7.某历史研究性学习小组开展研
- 名篇名句默写(8分) 【小题1】故夫 ,行比一乡,德合一君, ,其自视也
- 人类的人的眼色是由两对等位基因(AaBb)(二者独立遗传)共同决定的。在一个个体中,两对基因处于不同状态时,人的眼色如下
- 国务院新闻办公室发表《2010年中国人权事业的进展》白皮书,全面介绍了过去一年间我国在促进与保障公民各项基本人权方面作出
- 如下图是某种物质物态变化过程中温度随时间变化的图象,该图象反映的可能是 A.蜡的熔化过程
- 芳香族化合物A、B互为同分异构体,B的结构简式是 ,A经①②反应得C、D、E,B经①②步反应得E、F、H上述反应过
- 固定化酵母细胞发酵葡萄糖溶液时发现无酒精产生,原因不可能是( ) A.实验瓶盖了塞子
- 学校食堂为了让煤充分燃烧,达到节能减排之目的,正确合理的措施是() A. 增加煤的用量 B. 粉碎煤块 C. 提高锅炉的
- 已知:如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC相交于点D,DE⊥AB,垂足为E,ED的延长线与A
- 计算:
- 2.Please get ready to answer five questions in English. 1
- 下面漫画启示我们要()A. 以热爱祖国为荣,以危害祖国为耻 B. 以服务人民为荣,以背离人民为耻 C. 以辛勤劳动为荣,
- 下列关于动物细胞培养的叙述,正确的是() A.培养中的人效应T细胞能产生单克隆抗体 B.培养中的人B细胞能够无限地增殖
- 如图(甲)所示,光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R=0.4Ω,导轨上
- 下列物质中,能除去铁制品表面铁锈的是A.水 B.稀硫酸 C.氢氧化钠溶液 D



