初中 数学
计算a6×(a2)3÷a4的结果是( )
A . a3
B . a7
C . a8
D . a9
已知 和
和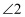 互余,
互余,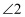 和
和 互余,
互余, , 则
, 则 ( )
( )
 和
和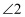 互余,
互余,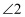 和
和 互余,
互余, , 则
, 则 ( )
( )
A . 65°
B . 25°
C . 115°
D . 155°
在平面直角坐标系  中,将点
中,将点  绕原点
绕原点  顺时针旋转90°,所得到的对应点的坐标为.
顺时针旋转90°,所得到的对应点的坐标为.
 中,将点
中,将点  绕原点
绕原点  顺时针旋转90°,所得到的对应点的坐标为.
顺时针旋转90°,所得到的对应点的坐标为.
已知a,b是一个等腰三角形的两边长,且满足a2+b2﹣6a﹣8b+25=0,则这个等腰三角形的周长为
.
如图,在四边形  中,对角线
中,对角线  和
和  相交于点O , 下列条件在不能判断四边形
相交于点O , 下列条件在不能判断四边形  是平行四边形的是( )
是平行四边形的是( )
 中,对角线
中,对角线  和
和  相交于点O , 下列条件在不能判断四边形
相交于点O , 下列条件在不能判断四边形  是平行四边形的是( )
是平行四边形的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知 ,
,  , 则
, 则 .
.
 ,
,  , 则
, 则 .
.
如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=  (k≠0)的图象经过点C.
(k≠0)的图象经过点C.
 (k≠0)的图象经过点C.
(k≠0)的图象经过点C.
-
(1) 求反比例函数的解析式;
-
(2) 若点P是反比例函数图象上的一点,△PAD的面积恰好等于正方形ABCD的面积,求点P的坐标.
若点P(m,1)在第二象限内,则点Q(1-m,-1)在( )
A . 第四象限
B . 第三象限
C . 第二象限
D . 第一象限
某鱼塘里养了1600条鲤鱼,若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,则该鱼塘捞到鲤鱼的概率约为( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列函数关系式中属于反比例函数的是( )
A .  B .
B .  C .
C .  D .
D . 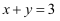
 B .
B .  C .
C .  D .
D . 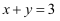
作图题:如图,已知  ,
,  (
(  )求作一个角使它等于
)求作一个角使它等于  (不写作法,保留作图痕迹,不在原图上作)
(不写作法,保留作图痕迹,不在原图上作)
 ,
,  (
(  )求作一个角使它等于
)求作一个角使它等于  (不写作法,保留作图痕迹,不在原图上作)
(不写作法,保留作图痕迹,不在原图上作) 
如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.



-
(1) 求证:∠ABC=∠ACB;
-
(2) 当D在线段BC上时,
①求证:△BAD≌△CAE;②当点D运动到何处时,AC⊥DE,并说明理由;
-
(3) 当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)
计算:①  ;②
;②  .③
.③  .
.
 ;②
;②  .③
.③  .
.
如图,已知:AB∥CD,DB⊥BC,∠1=40°,求∠2的度数.完成下面的证明过程:

证明:∵AB∥CD( ),
∴∠1=∠BCD=40°( ).
∵BD⊥BC,
∴∠CBD=_▲_.
∵∠2+∠CBD+∠BCD= ( ),
∴∠2=_▲_ .
同一平面内互不重合的三条直线的交点个数有 ____________ 个 .
![]() 如图,在△ABC中,AB+AC=6cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为 cm.
如图,在△ABC中,AB+AC=6cm,BC的垂直平分线l与AC相交于点D,则△ABD的周长为 cm.

已知![]() 的直径
的直径![]() 为
为![]() 上的一点,
上的一点,![]() ,则
,则![]() =
= ![]() .
.

已知一个正方体的体积是729立方厘米,现在要在它的8个角上分别截去8个大小相同的小正方体,使得截去后余下的体积是665立方厘米,则截去的每个小正方体的棱长是( )
A.8厘米 B.6厘米 C.4厘米 D.2厘米
已知线段AB=10cm,直线AB上有![]() 一点C,且BC=4cm,M是线段AC的中点,求AM的长.
一点C,且BC=4cm,M是线段AC的中点,求AM的长.
下面表格列出了函数y=ax2+bx+c(a,b、c是常数,且a≠0),部分x与y对应值,那么方程ax2+bx+c=0的一个根x的取值范围是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | ﹣0.03 | ﹣0.01 | 0.02 | 0.04 |
A.6<x<6.7 B.6.7<x<6.18 C.6.18<x<6.19 D.6.9<x<9.20
最近更新
- 在双链DNA分子中,有腺嘌吟n个,占全部碱基的比例为1/5,则该DNA分子中鸟嘌呤的个数是 A.0.25n
- 阅读下面文言文,完成小题。(19分) 君子曰:学不可以已。青,取之于蓝,而青于蓝;冰,水为之,而寒于水。木直中绳,輮(左
- 清咸丰年间,宁波附近海域海盗很多,已经缴过各种税费的商人和渔民们,面对水师的不作为,不得已自己凑钱激励水师。刚开始还管用
- ----Shall I give you a ride as you live so far away? ----Tha
- 在一个容积为6 L的密闭容器中,放入3 L X(g)和2 L Y(g),在一定条件下发生反应4X(g)+nY(g) 2Q
- 2.下列句子中没有语病的一项是( ) A.法国民航安全调查分析局(BEA)方面称,他们从德国之翼航空公司失事的A32
- 制约远西部地带发展的最重要经济原因是() A.资金不足、技术落后、人才匮乏 B. 农业基础薄弱 C.水土
- 科学家用含18O的葡萄糖来追踪需氧呼吸中的氧原子,发现其转移途径是( ) A.葡萄糖→丙酮酸→水
- 1931年1月31日在洛杉矶举行了《城市之光》首映式,卓别林和爱因斯坦站在一起,面对欢呼的人群,艺术之星对科学之星说:“
- 仙人掌和生活在珊瑚礁中的珊瑚鱼,组成它们的化学元素含量 A.差异很大 B.大体相同 C.很难确
- 2009年8月22日,生态文明贵阳会议开幕。积极建设生态文明,努力促进人与自然和谐,是经济社会发展全局赋予环境保护工作最
- 下列函数中,最小正周期为的偶函数为( ) (A) (B) (C)
- 短周期元素R的原子核外电子数等于核内中子数,该元素单质7.8g与氧气充分反应可生成13g化合物RO,则该元素的价电子层是
- 如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位
- 物质对应的化学式书写正确的是() A.碳酸钠﹣NaCO3 B.硫酸﹣H2SO4 C.氧化铁﹣FeO D.氢氧化钾﹣
- 根据表中数据,正确的分析是( ) 动物名称 心脏占体重比例% 每分钟心跳次数 蛙 0.57 22 人 0.42 7
- “西气东输”工程是根据我国资源分布不均,各地发展不平衡则做出的重大能源调配政策。它蕴含的哲理是 A.物质决定意识,一切从
- —________ the small town is!— Yes, it is more beautiful than
- 对化学平衡移动的分析,下列说法正确的是: A.已达平衡的反应C(s)+H2O(g)CO(g)+H2(g),当增加反应物的
- 根据力与运动的关系,下图中小明和小华的观点 A.小明正确 B.小华正确



