初中 数学
下列多项式是五次多项式的是( )
A . x3+y2
B . x2y3+xy+4
C . x5y﹣l
D . x5﹣y6+1
阅读第(1)题解答过程填理由,并解答第(2)题

-
(1) 已知:如图 1 AB∥CD,P 为 AB、CD 之间一点,求∠B+∠C+∠BPC的大小.
解:过点 P 作 PM∥AB
∵AB∥CD(已知)
∴PM∥CD
∴∠B+∠1=180°
∴∠C+∠2=180°
∵∠BPC=∠1+∠2
∴∠B+∠C+∠BPC=360°
-
(2) 我们生活中经常接触小刀,小刀刀柄外形是一个直角梯形(挖去一个小半圈)如图 2,刀片上、下是平行的,转动刀片时会形成∠1 和∠2,那么∠1+∠2 的大小是否会随刀片的转动面改变?说明理由.
化简
-
(1) ﹣3x2y+2x2y+3xy2﹣xy2
-
(2) 4x2﹣(2x2+x﹣1)+(2﹣x2+3x)
已知点  是线段
是线段  的黄金分割点,且
的黄金分割点,且  ,如果
,如果  ,那么
,那么  .
.
 是线段
是线段  的黄金分割点,且
的黄金分割点,且  ,如果
,如果  ,那么
,那么  .
.
某中学初三(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如下的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:

-
(1) 初三(1)班的学生人数为,并把条形统计图补充完整;
-
(2) 扇形统计图中m=,n=,表示“足球”的扇形的圆心角是度;
-
(3) 排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
小明在梳理平行四边形、矩形、菱形、正方形的性质时,发现它们的对角线都具有一个共同的性质,这条性质是对角线( )
A . 互相平分
B . 相等
C . 互相垂直
D . 平分一组对角
倒数等于本身的数是( )
A . 1
B . 0
C . -1
D . ±1
如图,在某一时刻测得1米长的竹竿竖直放置时影长1.2米,在同一时刻旗杆AB的影长不全落在水平地面上,有一部分落在楼房的墙上,他测得落在地面上影长为BD=9.6米,留在墙上的影长CD=2米,则旗杆的高度( )

A . 12米
B . 10.2米
C . 10米
D . 9.6米
下列实数 ,3.14,−
,3.14,− ,
,  −2 , 0.2020020002…,
−2 , 0.2020020002…,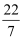 ,1.56,-|-π|,其中无理数有( )
,1.56,-|-π|,其中无理数有( )
 ,3.14,−
,3.14,− ,
,  −2 , 0.2020020002…,
−2 , 0.2020020002…,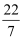 ,1.56,-|-π|,其中无理数有( )
,1.56,-|-π|,其中无理数有( )
A . 6个
B . 5个
C . 4个
D . 3个
已知5+  小数部分为m,11﹣
小数部分为m,11﹣  为小数部分为n,则m+n=.
为小数部分为n,则m+n=.
 小数部分为m,11﹣
小数部分为m,11﹣  为小数部分为n,则m+n=.
为小数部分为n,则m+n=.
如图,在边长为  个单位长度的小正方形组成的
个单位长度的小正方形组成的  的网格中,给出了格点(顶点为网格线的交点)
的网格中,给出了格点(顶点为网格线的交点)  ,
,  为过网格线的一条直线.
为过网格线的一条直线.
 个单位长度的小正方形组成的
个单位长度的小正方形组成的  的网格中,给出了格点(顶点为网格线的交点)
的网格中,给出了格点(顶点为网格线的交点)  ,
,  为过网格线的一条直线.
为过网格线的一条直线. 
-
(1) 作
 关于直线
关于直线  对称的
对称的 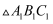 ;
;
-
(2) 求
 的面积.
的面积.
某校实验课程改革,初三年级设罝了A,B,C,D四门不同的拓展性课程(每位学生只选修其中一门,所有学生都有一门选修课程),学校摸底调査了初三学生的选课意向,并将调查结果绘制成两个不完整的统计图,问该校初三年级共有多少学生?其中要选修B、C课程的各有多少学生?、 

某金属零件如图所示,它的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C .
当  时,代数式
时,代数式  的值是
的值是 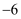 ,则当
,则当 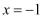 时,代数式
时,代数式  的值是.
的值是.
 时,代数式
时,代数式  的值是
的值是 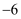 ,则当
,则当 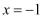 时,代数式
时,代数式  的值是.
的值是.
若|x+7|+|y+8|=0,则x+y=.
图为某地冬季一天的天气预报,这一天的温差是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影长为( )米.

A . 4
B . 5
C . 6
D . 7
下列各式中正确的是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
下列各点中,位于直角坐标系第二象限的点是( )
A.(2,1) B.(﹣2,﹣1) C.(2,﹣1) D.(﹣2,1)
如果代数式![]() 有意义,那么实数x的取值范围为_ _ _.
有意义,那么实数x的取值范围为_ _ _.
最近更新
- 设双曲线的右顶点为A,右焦点为F,过点F平行双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为。
- 股份有限公司和有限责任公司共同特征是 ( ) A.股份和无限
- 阅读《出师表》(节选),完成第12-15题。 先帝创业未半而中道崩殂,今天下三分,益州疲弊,此诚危急存亡之秋也。然侍卫之
- 有一条河流,河水流量为0.4m3/s,落差为5m,现利用它来发电,使用的发电机总效率为50%,发电机输出电压为250V,
- 在下面一段话空缺处依次填入成语,最恰当的一组是(3分) 散文的妙处真可说是 ,然而最高的理想也不过是“简单”
- 下列不属于旅游活动设计内容的是A.了解旅游者出游的愿望和能力B.多种渠道收集各种旅游地信息C.选择最有名的旅游地D.旅游
- 9的算术平方根是( ) A. 3 B.-3 C.±3 D
- 下列叙述正确的是() A.铝制容器可盛装热的浓硫酸 B.镁的金属性比铝的金属性强 C.氢氧化铝能溶于过量氨水 D.镁在空
- 至于负者歌于途,_______________,前者呼,后者应……(欧阳修《醉翁亭记》)
- 有下列8种物质.①甲烷 ②苯 ③环己烷 ④聚乙烯 ⑤聚异戊二烯 ⑥环己烯 ⑦2-丁烯 ⑧邻二甲苯,既能使酸
- 列车上有出售食品的手推车(如图6所示)。若货物在车内摆放均匀,当前轮遇到障碍物A时,售货员向下按扶把,这时手推车可以视为
- These dressare for 30%off . A. on sale B. in sal
- 下列关于细胞分裂叙述中正确的是( ) A.细胞分裂是不断的、无限的 B.生物体内任何细胞都具有分裂能力
- 若正数a,b满足+=1,则的最小值为() A.1
- “地无三尺平”是对哪个高原的真实写照( ) A.青藏高原 B.黄土高原 C.云贵高原
- 如果点在一次函数的图像上,则 .(填“>”,“<”或“=”)
- 读下面一首唐诗,回答问题 酬乐天扬州初逢席上见赠 刘禹锡 巴山楚水凄凉地,二十三年弃置身。怀旧空吟闻笛赋,到乡翻似烂
- 如图所示,d处固定有负点电荷Q,一个带电质点只在电场力作用下运动,射入此区域时的轨迹为图中曲线abc,a、b、c、d恰好
- I am looking forward to see all of you again in the near fut
- TheChinese Dream is ___________ dream to improve people's w



