初中 数学
各组人数统计表
组号 | 年龄分组 | 频数(人) | 频率 |
第一组 | 20≤x<25 | 50 | 0.05 |
第二组 | 25≤x<30 | a | 0.35 |
第三组 | 35≤x<35 | 300 | 0.3 |
第四组 | 35≤x<40 | 200 | b |
第五组 | 40≤x≤45 | 100 | 0.1 |

-
(1) 求本次调查的样本容量及表中的a、b的值;
-
(2) 调查结果得到对生产和居住环境满意的人数的频率分布直方图如图,政策规定:本次调查满意人数超过调查人数的一半,则称调查结果为满意.如果第一组满意人数为36,请问此次调查结果是否满意;并指出第五组满意人数的百分比;
-
(3) 从第二张和第四组对生产和居住环境满意的职工中分别抽取3人和2人作义务宣传员,在这5人中随机抽取2人介绍经验,求第二组和第四组恰好各有1人被抽中介绍经验的概率.

 的值为( )
的值为( )
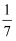 B . ﹣
B . ﹣  C .
C .  D . ﹣3
D . ﹣3

整数: 
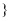
分数: 
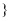
无理数: 
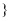
实数: 
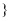
如图,某测量船位于海岛P的北偏西60°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处,求测量船从A处航行到B处的路程(结果保留根号).

 是
是  的外接圆,连结
的外接圆,连结  ,
,  ,且点
,且点  ,
,  在弦
在弦  的同侧,若
的同侧,若  ,则
,则  的度数为( )
的度数为( )
 B .
B .  C .
C .  D .
D . 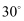
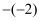 的结果是( )
的结果是( )
 C .
C .  D . 2
D . 2
已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

-
(1) 如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
-
(2) ①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC=
 ?请说明理由.
?请说明理由.
 ,则
,则  =
=
 ,
,  .
.
 ,并把解集表示在数轴上.
,并把解集表示在数轴上.
 的最简公分母是.
的最简公分母是.

 D . △ABC与△A′B′C′的相似比为
D . △ABC与△A′B′C′的相似比为
如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N。
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,当
,当![]() 为何值时,MN∥BE?
为何值时,MN∥BE?
在分析样本数据时,小华列出了方差的计算公式 
A .样本的容量是 3 B .中位数是 3 C .众数是 3 D .平均数是 3
- 棉、麻和真丝是很多纺织品的原料,它们都来自于生物体,其组成成分主要是 A.纤维素和脂肪
- 有学者指出:“美国思想体系的传统任何时候都不会转变为僵死的教条,而是在每一新的历史阶段为回答时代的呼唤而获得新生。”20
- ---Why didshe____________ your invitation? ---Because she ha
- 如表是小丽探究“光照是否影响种子萌发”时的有关操作和现象培养皿 操作1 操作2 操作3 现象 ① 在一层浸水的棉花上放等
- ---Goodbye, Joyce. Please remember me to yourparents. ---_
- 命题“,使得.”的否定是___________________.
- (陕西卷理16文16)某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三
- 小李找来《权利法案》《王位继承法》两份材料,他是为研究哪个主题准备的( ) A.英国的君主立宪制
- It is suggested____we should think twice before we act. A.as
- 燕麦胚芽鞘如下图处理,经过几天后,变化是A.向左弯曲 B.向右弯曲
- 物体在几个外力作用下恰做匀速直线运动,如果突然撤去其中一个力F3,则它可能做( ) A.匀速直线运动
- 下列加点熟语运用正确的一项是( ) A、接着,姜昆颇为激动地发了一通感慨:“我们中国专门有这么一帮人,惟恐天下不乱
- 阅读下文,完成下列小题。 爱心菜 鸡叫头遍的时候,老王和老伴就在大棚里忙活开了。 等到一畦畦白菜扳倒,老王的头上已经袅起
- 在的切线中,斜率最小的切线方程为 A B C D
- 在一定质量的甲溶液中逐渐加入乙至过量,反应过程中溶液的总质量与加入乙的质量关系,能用下图曲线表示的是序号 甲 乙 ① H
- My mother asks me ________ to a party withher. A.go
- 下列句中加点词语的意义、用法完全相同的一项是( ) 族秦者秦也,非天下也 楚人一炬
- Although they are good friends, Tom and Peter haven’t a thin
- 对已达化学平衡的反应:2X(g)+Y(g)2Z(g),减小压强时,对反应产生的影响是A.逆反应速率增大,正反应速率减小,
- (1)红军不怕远征难, 。 (2)天上闪烁的星星



