初中 数学
某学校组织篮球比赛,实行单循环制,共有36场比赛,则参加的队数为( )
A . 8支
B . 9支
C . 10支
D . 11支
 的算术平方根是,
的算术平方根是,  的立方根是。
的立方根是。
用一批完全相同的正多边形地砖铺地面,不能进行镶嵌的是( )。
A . 正三角形
B . 正四边形
C . 正六边形
D . 正八边形
若关于x的不等式组  恰有3个整数解,则字母a的取值范围是.
恰有3个整数解,则字母a的取值范围是.
 恰有3个整数解,则字母a的取值范围是.
恰有3个整数解,则字母a的取值范围是.
解方程:
-
(1)
 ;
;
-
(2)
 .
.
如图,AB⊥BC,DC⊥BC,点E在BC上,AE⊥DE,DC=1,BE=3,BC=5,则AB=.

如图,  ,
,  平分
平分  ,
,  ,
,  ,
,  ,有下列结论:
,有下列结论:
 ,
,  平分
平分  ,
,  ,
,  ,
,  ,有下列结论:
,有下列结论:
①  ;②
;②  平分
平分 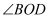 ;③
;③  ;④
;④  .
.
请将正确结论的序号填写在空中,并选择其一证明.
正确结论的序号是,我选择证明的结论序号是,证明:

如图,△ABC的周长为19, 点D、E在边BC上,∠ABC的平分线垂直于AE,垂足为N ,∠ACB的平分线重直于AD,垂足为M,若BC=7,则MN的长度为.

如图,在 中,中线AD、BE相交于点G,如果
中,中线AD、BE相交于点G,如果 , 那么
, 那么 (用含向量
(用含向量 的式子表示)
的式子表示)
 中,中线AD、BE相交于点G,如果
中,中线AD、BE相交于点G,如果 , 那么
, 那么 (用含向量
(用含向量 的式子表示)
的式子表示)
若点 关于y轴的对称点为
关于y轴的对称点为 , 则a+b=.
, 则a+b=.
 关于y轴的对称点为
关于y轴的对称点为 , 则a+b=.
, 则a+b=.
一次函数的图象过点(0,1),且函数y的值随自变量x的增大而减小,请写出一个符合条件的函数解析式.
解方程
-
(1) 5(x+2)=2(5x-1)
-
(2)

-
(3)

如图1,在平面直角坐标系中,直线l1:y=-x+5与x轴,y轴分别交于A、B两点。直线l2:y=-4x+b与l1交于点D(-3,8)且与x轴,y轴分别交于C、E。

-
(1) 求出点A坐标,直线l2的解析式;
-
(2) 如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿着线段PD以每秒
 个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
-
(3) 如图3,平面直角坐标系中有一点G(m,2),使得S△CEG=S△CEB , 求点G的坐标。
如图,长方形ABCD中放有6个形状、大小相同的长方形(空白区域),求图中阴影部分的面积.

小泽和小超分别用掷A,B两枚骰子的方法来确定P(x,y)的位置,她们规定:小泽掷得的点数为x,小超掷得的点数为  ,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
 ,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A .  B .
B .  C .
C . 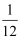 D .
D . 
 B .
B .  C .
C . 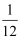 D .
D . 
分别在数轴上画出下列解集.
![]() ;
;
如图,一个四边形花坛![]() ,被两条线段
,被两条线段![]() 分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是
分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是![]() ,若
,若![]() ,
,![]() ,则有( )
,则有( )

A.![]() B.
B.![]() C.
C.![]() D.都不对
D.都不对
图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系得到的数学公式是_______________________________.

下列运算正确的是( )
A.a3•a4=a12 B.3a2•2a3=6a6
C.(﹣2x2y)3=﹣8x6y3 D.(﹣3a2b3)2=6a4b6
一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.![]() 米2 B.
米2 B.![]() 米2 C.(4+
米2 C.(4+![]() )米2 D.(4+4tanθ)米2
)米2 D.(4+4tanθ)米2

最近更新
- —You seemed toke deeply struck by his skill. —Not exactl
- 某科学家估测一个密度约为kg/m3的液态星球是否存在,他的主要根据之一就是它自转的周期,假若它存在,其自转周期的最小值约
- 谚语“苏湖熟、天下足”,反咉了中国南方经济发展水平超过北方的史实。这一现象最早发生在( )A.汉朝B.隋朝C.唐朝D.南
- 下图中能反映我国农业技术史上农用动力的一次革命的是( )
- In the hit film The bucket List, Jack Nicholson andMorgan Fr
- 如图所示,某同学用插针法测定一半圆形玻璃砖的折射率.在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线,并让入射光线过
- 已知A=B=R,x∈A,y∈B,f:x→y=ax+b,若5和20的原象分别是5和10,则7在f下的象f(7)=.
- 已知数列满足,(). (Ⅰ)判断数列是否为等比数列?若不是,请说明理由;若是,试求出通项; (Ⅱ)如果时,数列的前项和为
- 右图是元素周期表中的一格,依据图中的信息得到的下列认识错误的 是 A.该元素原子的质子数为14 B.该元素的相对原子质量
- 某超市用6800元购进A、B两种计算器共120只,这两种计算器的进价、标价如表.价格\类型 A型 B型 进价(元/只)
- 有些卫星因能量耗尽而报废,成为太空垃圾,所以被称为“垃圾卫星”。“轨道康复者”是“垃圾卫星”的救星,被称为“太空110”
- 下列句子中古今异义字判断及其解释错误的一项是【 】 A.吾以南面而君天下(古义:南面代称君主之位,面向南而坐;今义:
- 甲同学是个小马虎,以下内容摘自他的作业,其中没有错误的一组是 A (1)有的食品包装时充入氮气防腐 (2)把塑
- 读图回答下列问题。(10分)(1)图乙为图甲中A海域附近海底地形示意图,图中数字代表的地形名称为: ①_________
- 南偏东80°的射线与西南方向的射线组成的角(小于平角)是( ).C A.35° B
- 2010年6月21日,天文学家称,利用太空望远镜对太阳进行前所未有的详细观测和数据分析,发现太阳黑子及太阳的磁活动正在减
- 下列物质在水溶液中的电离方程式书写正确的是 A.CH3COOHH++CH3COO- B.NaHSO4===Na++HSO
- 苔痕上阶绿, 。 (《陋室铭》)
- 33.作文(共1小题) . 要求选准角度,明确立意,自选文体(诗歌除外),自拟标题;不要脱离材料内容及含意的范围作文
- “彩电冰箱平常货,手机相机百姓家”。改革开放30年来,人民群众的物质文化生活日新月异,各类具有现代气息,可以满足不同人群



