初中 数学
若m>-1,则多项式m3-m2-m+1的值为( )
A . 正数
B . 负数
C . 非负数
D . 非正数
如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/S的速度向点B运动,同时动点M从点N出发,沿线段BA以1cm/S的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)(  ),以点M为圆心,MB为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.
),以点M为圆心,MB为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.
 ),以点M为圆心,MB为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.
),以点M为圆心,MB为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.
-
(1) 求BF的长(用含有t的代数式表示),并求出t的取值范围;
-
(2) 当t为何值时,线段EN与⊙M相切?
-
(3) 若⊙M与线段EN只有一个公共点,求t的取值范围.
下列4个说法中:①直径是弦;②弦是直径;③任何一条直径所在的直线都是圆的对称轴;④弧是半圆; 正确的有( )
A . 1个
B . 2个
C . 3个
D . 4个
实数  +1的值在( )之间.
+1的值在( )之间.
 +1的值在( )之间.
+1的值在( )之间.
A . 0~1
B . 1~2
C . 2~3
D . 3~4
在 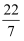 ,
,  ,-1.62,0这四个数中,有理数的个数为( ).
,-1.62,0这四个数中,有理数的个数为( ).
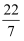 ,
,  ,-1.62,0这四个数中,有理数的个数为( ).
,-1.62,0这四个数中,有理数的个数为( ).
A . 4
B . 3
C . 2
D . 1
求式子中x的值:4(x﹣1)2﹣16=0.
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=  .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:

-
(1) 求sad60°的值;
-
(2) 对于0°<A<180°,求∠A的正对值sadA的取值范围.
-
(3) 已知sinα=
 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.
如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,求AE的长为多少?

阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在  中,
中,  ,
,  ,则
,则 

-
(1) 小天根据学习几何的经验,先画出了几何图形(如图1),他发现
 不是特殊角,但它是特殊角
不是特殊角,但它是特殊角  的一半,若构造有特殊角的直角三角形,则可能解决这个问题
的一半,若构造有特殊角的直角三角形,则可能解决这个问题  于是小天尝试着在CB边上截取
于是小天尝试着在CB边上截取  ,连接
,连接  如图
如图  ,通过构造有特殊角
,通过构造有特殊角  的直角三角形,经过推理和计算使问题得到解决.请回答:
的直角三角形,经过推理和计算使问题得到解决.请回答:  .
.
-
(2) 参考小天思考问题的方法,解决问题:
如图3,在等腰
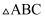 中,
中,  ,
,  ,请借助
,请借助 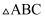 ,构造出
,构造出  的角,并求出该角的正切值.
的角,并求出该角的正切值.
不等式组  (x为未知数)无解,则函数y=(3−a)x2−x+
(x为未知数)无解,则函数y=(3−a)x2−x+ 图象与x轴( )
图象与x轴( )
 (x为未知数)无解,则函数y=(3−a)x2−x+
(x为未知数)无解,则函数y=(3−a)x2−x+ 图象与x轴( )
图象与x轴( )
A . 相交于两点
B . 没有交点
C . 相交于一点
D . 相交于一点或没有交点
下列运算正确的是( )
A . a2•a3=a6
B . 7a2﹣a2=7
C . ﹣ •(xy2)3=﹣4x3y6
D . (2m﹣n)2=4m2+n2
•(xy2)3=﹣4x3y6
D . (2m﹣n)2=4m2+n2
 •(xy2)3=﹣4x3y6
D . (2m﹣n)2=4m2+n2
•(xy2)3=﹣4x3y6
D . (2m﹣n)2=4m2+n2
如图,PA切⊙O于点A,PO交⊙O于点B,点C是优弧AB上一点,若∠ACB=35°,则∠P的度数是°.

规定a*b=5×a-  ×b(其中a,b是自然数),求
×b(其中a,b是自然数),求
 ×b(其中a,b是自然数),求
×b(其中a,b是自然数),求
-
(1) 10*6=,
-
(2) 6*10=
甲、乙两人在玩转盘游戏 时,游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜.如果指针落在分割线上,则需要重新转动转盘.

-
(1) 试用列表或画树形图的方法,求甲获胜的概率;
-
(2) 请问这个游戏规则对甲、乙双方公平吗?试说明理由.
将抛物线 在x轴上方的部分记为
在x轴上方的部分记为 , 在x轴上及其下方的部分记为
, 在x轴上及其下方的部分记为 , 将
, 将 沿x轴向下翻折得到
沿x轴向下翻折得到 ,
,  和
和 两部分组成的图象记为M.若直线
两部分组成的图象记为M.若直线 与M恰有2个交点,则m的取值范围为( )
与M恰有2个交点,则m的取值范围为( )
 在x轴上方的部分记为
在x轴上方的部分记为 , 在x轴上及其下方的部分记为
, 在x轴上及其下方的部分记为 , 将
, 将 沿x轴向下翻折得到
沿x轴向下翻折得到 ,
,  和
和 两部分组成的图象记为M.若直线
两部分组成的图象记为M.若直线 与M恰有2个交点,则m的取值范围为( )
与M恰有2个交点,则m的取值范围为( )
A .  或
或 B .
B .  或
或 C .
C .  D .
D .  或
或
 或
或 B .
B .  或
或 C .
C .  D .
D .  或
或
如图,小明在地面上放置一个平面镜  来测量铁塔
来测量铁塔  的高度,镜子与铁塔的距离
的高度,镜子与铁塔的距离  米,镜子与小明的距离
米,镜子与小明的距离  米时,小明刚好从镜子中看到铁塔顶端
米时,小明刚好从镜子中看到铁塔顶端  .已知小华的眼睛距地面的高度CD=1.6米,求铁塔
.已知小华的眼睛距地面的高度CD=1.6米,求铁塔  的高度.(根据光的反射原理,
的高度.(根据光的反射原理,  )
)
 来测量铁塔
来测量铁塔  的高度,镜子与铁塔的距离
的高度,镜子与铁塔的距离  米,镜子与小明的距离
米,镜子与小明的距离  米时,小明刚好从镜子中看到铁塔顶端
米时,小明刚好从镜子中看到铁塔顶端  .已知小华的眼睛距地面的高度CD=1.6米,求铁塔
.已知小华的眼睛距地面的高度CD=1.6米,求铁塔  的高度.(根据光的反射原理,
的高度.(根据光的反射原理,  )
) 
已知y与x2成正比例,且当x=3时,y=﹣18,写出y与x之间的函数解析式,它是二次函数吗?
一次函数  的图象经过(1,2),则反比例函数
的图象经过(1,2),则反比例函数  的图象经过点(2,).
的图象经过点(2,).
 的图象经过(1,2),则反比例函数
的图象经过(1,2),则反比例函数  的图象经过点(2,).
的图象经过点(2,).
解方程: x 2 - 6 x = 7
2a-5b-3a+b
最近更新
- I’vestarted driving again. I drove along a road ___21___ 12
- 已知二次函数的两个实数根分别是 (1)设函数的对称轴为 (2)如果
- Simon_________ his fingers when he was cooking the dinner.A
- 实验操作的规范是实验的基本要求下列实验操作正确的是()A.闻气体气味 B.点燃酒精灯 C.过滤 D.移开蒸发皿
- “我来自元谋,你来自周口,牵起你毛茸茸的手,爱让我们直立行走。”这首在网络上颇为流传的诗句,让我国境内的远古人类蒙上了
- 1945年,边区推广使用的《中学历史课本》讲义对唐太宗评价颇高。但很多教员认为“从人民的立场去看,评价不能只讲一面”“唐
- 将蚕豆根尖(细胞含6对染色体)制成装片后,高倍显微镜下可观察到 A. 复制后形成的24个DNA分子 B.位于细胞
- 在△ABC中,若b=,c=3,∠B=30°,则a=( ). A. B.2
- 能发生消去反应,生成物中存在同分异构体的是
- (07重庆市直属重点中学联考)下列有关酶的叙述错误的是 A.人成熟红细胞无细胞核、细胞内不能合成蛋白类酶 B
- Mr Smith _____me to buy several _____eggs for the dinner par
- 仔细观察下面这幅漫画,从多角度思考,说说它反映了怎样的社会现象。答:__________________________
- It is only by practising English for several hours every day
- 如果想了解菜粉蝶的生长发育知识,你会首先选择的书是A.《生物学》B.《蝴蝶》C.《无脊椎动物学》D.《昆虫学》
- 完成人类首次环球航行的是( ) A.葡萄牙人麦哲伦 B.意大利人
- You’d better open the window and let _____ some fresh air. A
- 一个多边形的内角和是外角和3倍,这个多边形是_________
- 国家发改委决定,自2010年12月22日零时起,汽油每吨上涨310元,93号汽油售价从之前的6.92元/升涨至7.17元
- 家兔体内产生黄脂或白脂是否受食物的影响?王老师选择健康的黄脂家兔和白脂家兔从事研究。他将两种兔子都分成两组,分别饲喂不同
- 阅读《春望》 国破山河在,城春草木深。感时花溅泪,恨别鸟惊心。 烽火连三月,家书抵万金。白头搔更短,浑欲不胜簪。 1、诗



