初中 数学
 是
是 的反比例函数( )
的反比例函数( ) B .
B .  C .
C .  D .
D . 
-
(1) 125x3=8
-
(2) (﹣2+x)2=9.
-
(1) ﹣5a+b+(6a﹣9b);
-
(2) ﹣5(3m+4n)+8(3m+4n).

 中,
中,  三个顶点坐标分别为A(-2,-4),B(-2,-1),C(-5,-2).
三个顶点坐标分别为A(-2,-4),B(-2,-1),C(-5,-2). 
-
(1) 请画出
 关于
关于 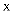 轴对称的
轴对称的 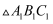 .
.
-
(2) 将
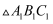 的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2 , B2 , C2 , 请画出
的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2 , B2 , C2 , 请画出  .
.
-
(3) 求
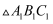 与
与  的面积相比,即
的面积相比,即  .(不写解答过程,直接写出结果).
.(不写解答过程,直接写出结果).
-
(1) 2﹣1+|1﹣
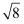 |+(
|+(  ﹣2)0﹣cos60°
﹣2)0﹣cos60°
-
(2) (2﹣
 )÷
)÷ 
-
(1)

-
(2)
 ÷
÷  .
.
-
(1) 4m2n3+2m3n3
-
(2) 2a2(b-2)-8b+16.
 的值,把它的分式和分母中的各项的系数都化为整数,则所得结果为
的值,把它的分式和分母中的各项的系数都化为整数,则所得结果为 
-
(1) 你认为图2中大正方形的边长为;小正方形(阴影部分)的边长为.(用含a、b的代数式表示)
-
(2) 仔细观察图2,请你写出下列三个代数式:(a﹣b)2 , (a+b)2 , ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
-
(3) 已知a+b=4,ab=3.求代数式a﹣b的值.
![]()
-
(1) 解方程:
 .
.
-
(2) 解方程:
 .
.
 |的相反数是( )
|的相反数是( )
 B . ﹣
B . ﹣ C . 3
D . -3
C . 3
D . -3
在实数范围内分解因式 
2021 年 7 月 24 日,中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》.某学校积极响应 “ 双减 ” 政策,为了丰富学生校园生活,经研究决定准备购买一批体育健身器材.已知购买 2 个篮球和 3 个排球共花费 440 元,购买 4 个篮球和 1 个排球共花费 480 元.

(1) 求篮球和排球的单价;
(2) 某体育用品店有两种优惠方案,方案一:每购买一个篮球就送一个排球;方案二:购买篮球和排球的费用一律打七五折.该学校需要购买 40 个篮球和 x 个排球( 


① 根据题目信息,直接写出 

② 画出 


③ 根据图象回答:当购买排球的数量 x 满足条件 时,方案二比方案一更优惠.
一个扇形的圆心角为120°,半径为3,则这个扇形的面积为 (结果保留π)
.∠α的补角比∠α的余角的3倍大10°,则∠α=__________.
一元二次方程x2-x=0的根是( )
A.x=1 B.x=0
C.x1=0,x2=1 D.x1=0,x2=-1
- 问答题 1.秦汉时期,我国的科学技术有哪些领先于世界的成就? 2.鲁迅说《史记》是“史家之绝唱,无韵之离骚”,这是为什么
- (1)在浓硝酸中放入铜片。 ①开始反应的化学方程式为__________________________________
- 小明对“斜面的机械效率与什么因素有关?”这一课题,提出了如下一些值得探究的猜想:①斜面的机械效率与斜面的倾斜程度有关;②
- 短文填空 根据短文内容,选择适当的单词或短语填空,使短文意思完整。每个选项至多使用一次,有两项剩余。A. first
- 已知点是圆上的一个动点,点的坐标为,当在圆上运动时,线段的中点的轨迹是什么?
- 已知函数f(x)=(ex-e-x)x,f(log5x)+f(logx)≤2f(1),则x的取值范围是
- She sat there without her shoes on, ________. A. watchin
- 藏文史籍《萨加世系史》载:“元帝辖十一省,西藏之地面虽不足一省,但因为它是八思巴的住地和教法所在,故作为一省委付与八思巴
- 早期的殖民掠夺对欧洲产生的最大影响是 ( ) A. 增强了殖民国家的军事实力 B. 满足了封建主的奢侈生活
- 若tanα+cotα=3,则sinαcosα=____________,tan2α+cot2α=____________
- 2010年全国八大文物艺术品拍卖公司拍卖会成交额达242.5亿元,比2009年增加了2.8倍。八家公司单件成交额超千万元
- 下列说法中正确的是A.处于最低能量的原子叫做基态原子B.3p2表示3p能级有两个轨道C.同一原子中,1s、2s、3s电子
- 绿色植物在光下可以进行的生命活动有①光合作用 ②呼吸作用 ③蒸腾作用 ④根的吸收作用A.①② B
- 在如图所示的电路中,电源电压保持不变。电路中滑动变阻器上标有“20W 2A”字样,电流表的量程为0~0.6安,电压表的
- 下图表示有关蛋白质分子的概念图,下列对图示分析不正确的是( )A.一个多肽中A的种类一般最多有20种
- . _____ can be enjoyed until you have a deep understanding o
- 已知命题方程表示焦点在轴上的椭圆,命题关于的方程无实根,若“∧”为假命题,“∨”为真命题,求实数的取值范围.
- 阅读下列材料 材料一:我给了一般人民以恰好足够的权力,也不使他们失掉尊严,也不给他们太多;而那些有钱有势的豪富的人们,我
- 如图 ,四边形 ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为( ) A.50°
- 央视《新闻1+1》2010年5月4日播出了《校园安全:揪心!用心!放心!》,面对40天内发生的5起校园血案,中央提出,要



