初中数学：七年级　 八年级　 九年级　 中考　

初中数学

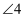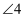如图，直线 $\text{[math]}$ 被直线 $\text{[math]}$ 所截，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

△ABC中，已知AB＝1，AC＝2．要使∠B是直角，BC的长度是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$ 或 $\text{[math]}$

下列说法正确的是( )

A . 一组对边平行，另一组对边相等的四边形是平行四边形 B . 对角线相等的平行四边形是菱形 C . 三个角都是直角的四边形是矩形 D . 一组邻边相等的平行四边形是正方形

长方形的长是a米，宽比长的2倍少b米，则宽为米．

如图，平面内有A、B、C、D四点，按照下列要求画图：

（1）顺次连接A、B、C、D四点，画出四边形ABCD；
（2）连接AC、BD相交于点O；
（3）分别延长线段AD、BC相交于点P；
（4）以点C为一个端点的线段有条；
（5）在线段BC上截取线段BM=AD+CD，保留作图痕迹．

如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，则其主视图可能是（）

A .

B .

C .

D .

现有点数为2，3，4，5的四张扑克牌，背面朝上洗匀，然后从中任意抽取两张，这两张牌上的数字之差为偶数的概率是.

因式分解：2a²﹣8=．

抛物线L：y=﹣x²+bx+c经过点A（0，1），与它的对称轴直线x=1交于点B.

图片_x0020_13

（1）直接写出抛物线L的解析式；
（2）如图1，过定点的直线y=kx﹣k+4（k＜0）与抛物线L交于点M、N.若△BMN的面积等于1，求k的值；
（3）如图2，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L₁ ，抛物线L₁与y轴交于点C，过点C作y轴的垂线交抛物线L₁于另一点D.F为抛物线L₁的对称轴与x轴的交点，P为线段OC上一点.若△PCD与△POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标.

已知函数y＝8x－11，要使y＞0，那么x应取( )

A . x＞

B . x＜

C . x＞0 D . x＜0

如图，在边长为4的正方形 $\text{[math]}$ 中，以点 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 为半径画弧，交对角线 $\text{[math]}$ 于点 $\text{[math]}$ ，则图中阴影部分的面积是（结果保留 $\text{[math]}$ .