初中 数学
我们新定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
-
(1) 理解并填空:
①根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?(填“是”或“不是”)
②若某三角形的三边长分别为1、
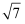 、2,则该三角形(填“是”或“不是”)奇异三角形.
、2,则该三角形(填“是”或“不是”)奇异三角形. -
(2) 探究:在
 中,两边长分别是
中,两边长分别是 , 且
, 且 ,
,  , 则这个三角形是否是奇异三角形?请说明理由.
, 则这个三角形是否是奇异三角形?请说明理由.
①最大的负整数是﹣1;
②数轴上表示数2和﹣2的点到原点的距离相等;
③当a≤0时,|a|=﹣a成立;
④a+5一定比a大.

请根据图中信息,解答下列问题:
-
(1) 参加初赛的选手共有名,请补全频数分布直方图;
-
(2) 扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
-
(3) 学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
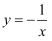 的图象上有两点
的图象上有两点  ,
,  ,若
,若  ,则下列结论正确的是( )
,则下列结论正确的是( )
 B .
B .  C .
C .  D .
D . 
 的一元二次方程x2-(k+3)x+2k+2=0.
的一元二次方程x2-(k+3)x+2k+2=0.
-
(1) 求证:方程总有两个实数根;
-
(2) 若方程有一根小于1,求k的取值范围.
 图象经过点(5,-1),该函数图象在( )
图象经过点(5,-1),该函数图象在( )
 :
:  D . 三个内角度数比为2:3:4
D . 三个内角度数比为2:3:4
 且平行于直线
且平行于直线 的直线有( )
的直线有( )

一次越野跑中,当李明跑了1600米时,小刚跑了1450米,此后两人匀速跑的路程s(米)与时间t(秒)的关系如图,结合结合图象,求图中S1和S0的位置.

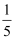 B . ﹣
B . ﹣ 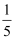 C . 5
D . ﹣5
C . 5
D . ﹣5
求证:EF和BD互相平分.

 ,
,  ,
,  C . 9,12,15
D . 7,20,24
C . 9,12,15
D . 7,20,24

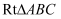 中,
中,  ,
,  ,且AC边在直线a上,将
,且AC边在直线a上,将  绕点A顺时针旋转到位置①可得到点
绕点A顺时针旋转到位置①可得到点  ,此时
,此时  ;将位置①的三角形绕点
;将位置①的三角形绕点  顺时针旋转到位置②,可得到点
顺时针旋转到位置②,可得到点  ,此时
,此时  ;将位置②的三角形绕点
;将位置②的三角形绕点  顺时针旋转到位置③,可得到点
顺时针旋转到位置③,可得到点  ,此时
,此时  ,…,按此规律继续旋转,直至得到点
,…,按此规律继续旋转,直至得到点  为止,则
为止,则  .
. 
(1)先阅读,再填空:
(x+5)(x+6)=x2+11x+30;
(x-5)(x-6)=x2-11x+30;
(x-5)(x+6)=x2+x-30;
(x+5)(x-6)=x2-x-30.
观察上面的算式,根据规律,直接写出下列各式的结果:
(a+90)(a-100)=____________; (y-80)(y-90)=____________.
(2)先阅读,再填空:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
观察上面各式:①由此归纳出一般性规律:
![]() ________;
________;
②根据①直接写出1+3+32+…+367+368的结果 ____________.
当x=3时,代数式ax2-3x-4的值为5,则字母a的值为 ( )
A.0 B.1 C.2 D.-2
如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.

(1)求抛物线解析式及点D坐标;
(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平行四边形,求此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
下列平面图形中,不是轴对称图形的是( )
A.
 B.
B.
 C.
C.
 D.
D.

- 下列化学用语表示正确的是() A.两个氢原子:2H B.碳酸钠:NaCO3 C.镁离子:Mg+2 D.氧元素显﹣2
- _____ we shall attend the meeting hasn’t been decided yet. A
- 市售加碘盐是在食盐中加入一定量的碘酸钾(KIO3),KIO3中碘元素的化合价是() A.+5
- (09深圳市调研)图示不同二氧化碳浓度下温度对光合作用速率影响曲线。分析曲线判断下列说法错误的是 A.光合作用同时
- 请给下面加点字注音。 寂寥() 彷徨() 彳亍() 颓圮() 笙箫()
- 一工棚的油毡层顶上有一个小孔,太阳光通过它后落在地面上形成一个圆形光斑,这一现象表明( )A.小孔的形态一定是圆的
- 下列化学用语既能表示一种元素,又能表示一个原子,还能表示一种物质的是()A. N2 B. Zn C. O D. 2H
- 24.在小白兔的细胞中,具有双层膜结构的是( ) A.线粒体 B.叶绿体和线粒体 C.高尔基体和叶
- 下列实验方案设计中,可行的是 A.在水中加入氯化铁晶体,加热至沸腾,可得到氢氧化铁胶体 B.氢氧化铁胶体中的H+、Cl-
- 如图所示,在xOy平面内有一个以O为圆心、半径R=0.1m的圆,P为圆周上的一点,O、P两点连线与x轴正方向的夹角为θ。
- 下列有关实验的叙述中,合理的是( ) ①用pH试纸测得某新制氯水的pH为2;②不宜用瓷坩埚灼烧氢氧化钠固体;③使用容量
- (2013武汉摸底)甲、乙两个物体从同一地点沿同一方向做直线运动,其v一t图象如图所示。关于两车的运动情况,下列说法正确
- 15~18世纪是欧美主要国家出现社会巨变的时代。这里的“社会巨变”主要是指 A.人文主义取代专制主义
- 函数在处取到极值,那么实数的值为 A.—2 B.2
- (2010山东文数)(1)已知全集,集合,则= A. B.C. D.
- 东有长三角,南有珠三角,北有环渤海,2009年7月9日,川、陕、渝三省市在重庆共同签署“西三角经济圈”工商联战略合作框架
- 高三学生即将毕业,请仿照例句为辛勤工作的老师们写毕业献辞(主体部分为两句话)表达肺腑之言。要求:①任选某一学科教师,突出
- 将少量灰黑色的生铁粉末,投入盛有过量稀硫酸的烧杯中,充分搅拌,待完全反应后过滤,滤纸上留有黑色的残渣。该黑色残渣的主要成
- 假设在北半球各高度水平气压梯度力相同,自地面向上一定高度内,风的变化情况为() A.风速变小,风向不变 B.风速变大,风
- HOLIDAY FUN AT THE POWERHOUSE 500 HARRIS STREET ULTIMO ·TELE



