初中 数学
如图1,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.

-
(1) 求证:BD=EC.
-
(2) 探究线段BD,DC,AD之间的数量关系并说明理由.
-
(3) 如图2,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=8,CD=4,求AD的长.
下面图形:四边形,三角形,梯形,平行四边形,菱形,矩形,正方形,圆,从中任取一个图形既是轴对称图形又是中心对称图形的概率是.
运输公司要把120吨物资从A地运往B地,有甲,乙,丙三种车型供选择,每种型号的车辆的运载量和运费如下表所示.(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
运载量(吨/辆) | 5 | 8 | 10 |
运费(元/辆) | 450 | 600 | 700 |
解答下列问题:
-
(1) 安排甲型车8辆,乙型车5辆,丙型车辆可将全部物资一次运完;
-
(2) 若全部物资仅用甲、乙型车一次运完,需运费9600元,则甲、乙型车各需多少辆?
-
(3) 若用甲、乙,丙型车共14辆同时参与运送,且一次运完全部物资,则三种型号的车各需多少辆?此时总运费为多少元?
因式分解3y2﹣6y+3,结果正确的是( )
A . 3(y﹣1)2
B . 3(y2﹣2y+1)
C . (3y﹣3)2
D . 

某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
|
发言次数n |
|
|
A |
0≤n<3 |
|
B |
3≤n<6 |
|
C |
6≤n<9 |
|
D |
9≤n<12 |
|
E |
12≤n<15 |
|
F |
15≤n<18 |

-
(1) 求样本容量,并补全直方图;
-
(2) 该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
-
(3) 已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
如图,圆柱形容器高为18cm,底面圆周长为24cm,在杯内璧离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为cm

如图,已知四边形  是平行四边形,E是
是平行四边形,E是  延长线上一点且
延长线上一点且  ,连接
,连接 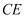 ,
,  .
.
 是平行四边形,E是
是平行四边形,E是  延长线上一点且
延长线上一点且  ,连接
,连接 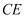 ,
,  .
. 
-
(1) 求证:四边形
 是平行四边形
是平行四边形
-
(2) 连接
 ,若
,若  ,
,  ,求
,求  的面积.
的面积.

-
(1) 如图1,点A和点B是直线
 上两点,点C和点D是直线
上两点,点C和点D是直线  上两点,且
上两点,且  ,BC⊥AB,若AB=2,BC=3,则△ABD的面积为;
,BC⊥AB,若AB=2,BC=3,则△ABD的面积为;
-
(2) 如图2,在边长为4的菱形ABCD中,∠A=60°,M是边AD的中点,N是边AB上一动点,将△AMN沿直线MN翻折得到△PMN,求点P到直线BC的最小距离;
-
(3) 如图3,在矩形ABCD中,AD=6,AB=8,E,F分别为边CB,CD上的动点,且EF=4,点O为EF的中点,连接BO并延长交CD于点M,过点O作ON∥DC交DB于点N,连接MN,则△BMN面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
已知一元二次方程  的较小根为x1 , 则下面对x1的估计正确的是
的较小根为x1 , 则下面对x1的估计正确的是
 的较小根为x1 , 则下面对x1的估计正确的是
的较小根为x1 , 则下面对x1的估计正确的是
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示的方格纸中,每个小方格的边长都是1,点A(﹣4,1)、B(﹣3,3)、C(﹣1,2).

⑴作△ABC关于y轴对称的△A'B'C';
⑵在x轴上找出点P , 使PA+PC最小,在图中描出满足条件的P点(保留作图痕迹),并直接写出P点的坐标.
某消防部队进行消防演练.在模拟现场,有一建筑物发生了火灾,消防车到达后,发现离建筑物的水平距离最近为12 m,如图,即AD=BC=12 m,此时建筑物中距地面12.8 m高的P处有一被困人员需要救援.已知消防云梯车的车身高AB是3.8 m,问此消防车的云梯至少应伸长多少米?

如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有.
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
②I到△ABC三个顶点的距离相等;
③∠BIC=90°+  ∠BAC;
∠BAC;
④点D是△BIC的外心.

学校为在汉语听写大赛中获得一、二等奖共30名学生购买奖品,其中一等奖奖品每份80元,二等奖奖品每份60元,共花费了2000元,获一等奖、二等奖的学生分别是多少?
如图,射线 是北偏西
是北偏西 方向,射线
方向,射线 平分
平分 , 则
, 则 的度数为( )
的度数为( )
 是北偏西
是北偏西 方向,射线
方向,射线 平分
平分 , 则
, 则 的度数为( )
的度数为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若![]() ,
,![]() 为有理数,现规定一种新运算“⊕”,满足
为有理数,现规定一种新运算“⊕”,满足![]() ⊕
⊕![]() ,
,
则(2⊕3)⊕(-3)的值是
先化简,再求值:![]() ,其中
,其中![]() ,
,![]() .
.
如图,将6个大小、形状相同的等腰梯形和2个全等的等边三角形密铺成一个四边形,这个四边形的最大内角等于 .

如图,二次函数y=-![]() x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.

(1)求此二次函数的解析式;
(2)证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图像及x轴于Q、H两点,试问:是否存在这样的点 P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8:00从同一地点出发,请你根据图中给出的信息预测,乌龟在__________点追上兔子.

-64的立方根是( )
![]() A.-4 B.8 C.-4和4 D. -8和8
A.-4 B.8 C.-4和4 D. -8和8
最近更新
- 许多人购物和旅游时经常使用信用卡。。信用每作为电子货币的一种,在使用过程中执行的货币职能有
- ((08潍坊))如图所示,是小明同学探究“怎样产生感应电流”的实验装置.ab是一根铜棒,通过导线连接在灵敏电流计的两接线
- 我国古代农耕经济形成南稻北粟局面取决于 A.自然条件 B.政府政策 C.居民口味
- 已知集合 A. B.
- 下列各个句子没有语病的一句是(3分) A.我们仔细调查研究的结果,认为他要负全部责任,但他却百般抵赖,拒不承担由于酒后开
- 一个两位数,个位数字比十位数字大3,个位数字的平方刚好等于这个两位数,则这个两位数是________.
- ()(本小题满分10分) 已知等差数列{}中,求{}前n项和. w.w.w.k.s.5.u.c.o.m
- 下列关于“校园生物调查”的叙述中,不正确的是( ) A.调查生物可不必太注意草丛和落叶里的小生物,只须注意较大的
- 下列词语中没有错别字的一组是( ) A、谛造 矫键 四不像 解铃还须系铃人 B、渲泄 内
- 下列事例中的物态变化,属于液化现象的是 A.从冰箱中取出的冰块化成水 B.冬天,藏眼镜的人从室外进入温暖的室
- (·宁夏银川实验中学高三上第一次月考)Finally she got too tired and fell asleep
- 小明在元素周期表中查找到如图所示的﹣格后,明白了不能把一氧化碳写成“Co”的原因. (1)“Co”表
- 生活中的下列物质属于纯净物的是【 】 A.米酒 B. 纯碱 C.食醋
- 33、右图是生态系统中碳循环示意图,“→”表示碳的流动方向,下列说法正确的是()A.图中A是生产者,B、D、E是消费者,
- 阅读理解;根据短文内容,选择最佳选项。Kiteshave a long history. They may date
- “迟至1863年,中国的皇帝致函林肯,告知中国致力于保持与美国的友好关系……发此函时,中国已经输掉了与西方列强的两场战
- 俄国工人雅可夫认识到当前俄国革命的任务是要从资产阶级民主革命过渡到无产阶级的社会主义革命,是在经历了哪个事件后 A.二月
- In spite of repeated wrongs done to him, he looks _____ to p
- 下列实验操作正确的是() A. 倾到液体 B. 读取体积 C. 点燃酒精灯 D. 滴加液体
- 较大剂量注射一种激素后,小白鼠渐渐反应迟钝,活动减少,以至昏睡,该激素是 A.甲状腺激素 B.雄性激素



