初中 数学
小韦同学周末的红色之旅,坐爸爸的车去百色起义纪念馆,从家里行驶7千米后,进入高速公路,在高速公路上保持匀速行驶,小韦记录高速公路上行驶的时间(和路程)数据如下表,按照这个速度行驶了2小时进入高速路出口匝道,再行驶5千米抵达纪念馆,则小韦家到纪念馆的路程是千米.
|
t小时 |
0.2 |
0.6 |
0.8 |
|
s千米 |
20 |
60 |
80 |
如图,从点A到点B的四条路径中,A、B两点之间的距离指的是路径的长度.(填序号)

已知:关于x的一元二次方程x2+ax+a﹣2=0.
-
(1) 求证:无论a取任何实数,此方程总有两个不相等的实数根;
-
(2) 当方程的一个根为﹣2时,求方程的另一个根.
如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图面积是( )

A . 3
B . 4
C . 5
D . 6
某厂为满足市场需求,改造了10条口罩生产线,每条生产线每天可生产口罩500个.如果每增加一条生产线,每条生产线每天就会少生产20个口罩.设增加x条生产线(x为正整数),每条生产线每天可生产口罩y个.
-
(1) 请直接写出y与x之间的函数关系式和自变量取值范围;
-
(2) 设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出当x为多少时,每天生产的口罩数量w最多?最多为多少个?
如果t>0,那么a+t与a的大小关系是( )
A . a+t>a
B . a+t<a
C . a+t≥a
D . 不能确定
如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.

-
(1) 求证:△CBE为等边三角形;
-
(2) 若AD=5,DE=7,求CD的长.
如图,一次函数  与函数
与函数  的图象交于
的图象交于  ,
,  两点,
两点,  轴于C,
轴于C,  轴于D
轴于D
 与函数
与函数  的图象交于
的图象交于  ,
,  两点,
两点,  轴于C,
轴于C,  轴于D
轴于D 
-
(1) 求k的值;
-
(2) 根据图象直接写出
 的x的取值范围;
的x的取值范围;
-
(3)
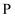 是线段AB上的一点,连接PC,PD,若
是线段AB上的一点,连接PC,PD,若  和
和  面积相等,求点P坐标.
面积相等,求点P坐标.
已知:如图,AD=BC,AB=DC,求证:∠A=∠C.

在一个布袋内有大小、质量都相等的球20个,其中红球6个,从中任取1个,取到红球的概率为( )
A . 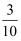 B .
B .  C .
C .  D .
D . 
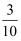 B .
B .  C .
C .  D .
D . 
-
(1) 解方程组:

-
(2) 解不等式组:
 ,并把解集表示在数轴上.
,并把解集表示在数轴上.

在平面直角坐标系中,若点P(m﹣3,m+1)在第二象限,则m的取值范围为 .
在实数范围内因式分解:a2-2=.
我国传统文化中的“福禄寿喜”图由下面四个图案构成.这四个图案中既是轴对称图形,又是中心对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算  的结果是( )
的结果是( )
 的结果是( )
的结果是( )
A .  B . -1
C .
B . -1
C .  D . 1
D . 1
 B . -1
C .
B . -1
C .  D . 1
D . 1
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=.

下列一元二次方程中,两根之和为2的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.
 |
已知α是一元二次方程x2﹣x﹣1=0较大的根,则下面对α的估计正确的是( )
A. 0<α<1 B. 1<α<1.5 C. 1.5<α<2 D. 2<α<3
解方程:![]()
最近更新
- 只用一种试剂就能区别下列四种溶液:NaHCO3 、NaCl、 Na2SO3 、 BaCl2 ;则该试剂应是_______
- 指出:“中国国民党和中国领导的抗日军队,分别担负着正面战场和敌后战场的作战任务,形成了共同抗击日本侵略者的战略态势。”下
- 下列四个命题: (1)“”的否定; (2)“若”的否命题; (3)在中,“”是“”的充分不必要条件; (4)“函数为奇函
- 罗斯福在1932年4月的一次全国广播讲话中说:“在这个不幸的时代,我们要制订出一些计划来,把希望重新寄托在那些压在经济金
- 物质的性质与用途密切相关,下列说法错误的是( ) A.冰箱内放置木炭可除异味 B.氢氧化钠
- 向饱和NaOH溶液中加入一定量Na2O2,充分反应后恢复到原温度下列说法正确的是 A.有晶体析出,原溶液质量不变
- 在2008年汶川地震中,位于成都平原的一座2000多年前的大型水利工程经受住了考验,充分体现了中华民族的伟大智慧。这一著
- 在古代孔子提出过“以德治民”的主张,现在党和政府提倡“以德治国”。说明( )A.无论任何时代,我们遵循的道德准则是一致的
- 法律制度是人类文明的重大成果,是几千年来文明沉淀的精华,从古至今,法律制度的发展完善,也是人类文明进步的一个缩影,读图回
- 设f(n)=,n∈N*,那么f(n+1)-f(n)=()
- 23.中秋节是我国的传统节日之一,请根据下面的图示把中秋节的有关情况写成一段话,要求内容完整,表述准确,语言连贯,不超过
- It's time to be water efficient! As populations increase a
- 下列各句标点符合的使用正确的一项是( ) A. 哪里是山?哪里是房屋,哪里是菜园?我终于分辨出来了。 B. 青松,
- 从可持续发展的观点来看,“”时期遭到破坏最严重的是( ) A.农业 B.工业 C.教育
- (2015·衡水高三调,16)截面为直角三角形的木块A质量为M,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面
- 下列物质中,既能跟盐酸反应,又能跟NaOH溶液反应的化合物是( ) ①Al ②Al2O3 ③Al(OH)3 ④
- 根据下面规定的情境写一段话,不能少于30个字。 情境:赛场 国歌 热泪
- A lot of us lose life's tough battles by starting afrontal(正
- (11·西宁)(本小题满分10分)国家发改委公布的《商品房销售明码标价规定》,从2011年5月1日起商品房销售实行一套一
- 下列四幅风带图中,对西欧温带海洋性气候的形成有重要影响的是:A B C



