初中数学：七年级　 八年级　 九年级　 中考　

初中数学

甲乙丙三个商店都在销售同一种排球，而且每个球的标价都是25元．但三个店的促销方式不一样：甲店的促销方式是每买十送二，乙店的促销方式是优惠16%，丙店的优惠方式是买球每满100元可返现金15元．学校准备买60个这种排球．你认为到家商店买比较省钱，这时实际只需要付元．

下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

已知 $\text{[math]}$ 的算术平方根是3，b是8的立方根，c是 $\text{[math]}$ 的整数部分.

（1）求 $\text{[math]}$ 的值.
（2）求 $\text{[math]}$ 的平方根.

如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连结CE交AD于点F，连结BD交CE于点G，连结BE. 下列结论中：① CE=BD=2；②△ADC是等腰直角三角形；③∠ADB=∠AEB； ④ CD·AE=EF·CG；一定正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

下列对二次函数 $\text{[math]}$ 的图象的描述，正确的是（）

A . 开口向下 B . 对称轴是 $\text{[math]}$ 轴 C . 经过原点 D . 在对称轴右侧 $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小

若一个直角三角形的两边长分别是4cm，3cm，则第三条边长是 cm．

小学时候大家喜欢玩的幻方游戏，老师稍加创新改成了“幻圆”游戏，现在将-1、12、-3、14、15、-2、-4、13分别填入图中的圆圆内，使横、竖以及内外两围上的 4个数字之和都相等，老师已经帮助同学们完成了部分填空，则图中a+b的值为（）

A . 12 或-3 B . -15或 13 C . 12 或-16 D . -15或11

某校七年级学生开展外出研学活动，准备租用45座和60座两种车型，若租用45座车正好坐满，若租用60座车就少租一辆，并且有一辆没坐满，但超过一半，你知道学校七年级有多少学生吗？

已知x是 $\text{[math]}$ 的整数部分，y是 $\text{[math]}$ 的小数部分，求x（ $\text{[math]}$ ﹣y）的值．

如果 $\text{[math]}$ 是方程ax+（a﹣2）y=0的一组解，则a的值（）

A . 1 B . 2 C . ﹣1 D . ﹣2

已知单项式号 $\text{[math]}$ 的次数是5.则 $\text{[math]}$ .

如图，已知△ABC中，AB＝AC，∠BAC＝90°，BF⊥AD垂足为E，连接DF，若S_△ADF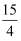＝ $\text{[math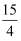]}$ ，∠AFB＝∠CFD，则DF的长为．

若单项式 $\text{[math]}$ 与 $\text{[math]}$ 的和仍为单项式，则其和为.

甲、乙两人共同计算一道整式：（x+a）（2x+b），由于甲抄错了a的符号，得到的结果是2x²-7x+3，乙漏抄了第二个多项式中x的系数，得到的结果是x²+2x-3．

（1）求a，b的值；（2）请计算这道题的正确结果

——(—)

乘火车从A站出发，沿途经过3个车站方可到达B站，那么在A、B两站之间需要安排不同的车票种．

方程x²﹣5x=0的根是（　　）

A．x₁=0，x₂=5 B．x₁=0，x₂=﹣5 C．x=0 D．x=5

当x=　　　　　　时，代数式3x﹣6与2x+1的值互为相数．

　

人的身高h随时间t的变化而变化，那么下列说法正确的是（　　）

A．h，t都是不变量 B．t是自变量，h是因变量

C．h，t都是自变量 D．h是自变量，t是因变量

最近更新

　