初中 数学
已知  与x成正比,且当
与x成正比,且当  时,
时, 
 与x成正比,且当
与x成正比,且当  时,
时, 
-
(1) 求y与x之间的函数关系式;
-
(2) 若点
 在这个函数图象上,求m的值
在这个函数图象上,求m的值
正整数按如下图的规律排列,请写出第15行,第17列的数字是。

阅读下列推理过程,将空白部分补充完整.

-
(1) 如图1,∠ABC=∠A1B1C1 , BD,B1D1分别是∠ABC,∠A1B1C1的角平分线,对∠DBC=∠D1B1C1进行说理.
理由:因为BD,B1D1分别是∠ABC,∠A1B1C1的角平分线
所以∠DBC=,∠D1B1C1=(角平分线的定义)
又因为∠ABC=∠A1B1C1
所以
 ∠ABC=
∠ABC=  ∠A1B1C1
∠A1B1C1所以∠DBC=∠D1B1C1()
-
(2) 如图2,EF∥AD,∠1=∠2,∠B=40°,求∠CDG的度数.
因为EF∥AD,
所以∠2=()
又因为∠1=∠2 (已知)
所以∠1=(等量代换)
所以AB∥GD()
所以∠B=()
因为∠B=40°(已知)
所以∠CDG=(等量代换)
-
(3) 下面是“积的乘方的法则“的推导过程,在括号里写出每一步的依据.
因为(ab)n=
 ()
()=
 ()
()=anbn()
所以(ab)n=anbn .
如图,菱形  的边
的边  在
在  轴上,点
轴上,点  的坐标为
的坐标为 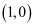 ,点
,点  在反比例函数
在反比例函数  (
(  )的图象上,直线
)的图象上,直线  经过点
经过点  ,与
,与  轴交于点
轴交于点  ,连接
,连接  ,
,  .
.
 的边
的边  在
在  轴上,点
轴上,点  的坐标为
的坐标为 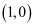 ,点
,点  在反比例函数
在反比例函数  (
(  )的图象上,直线
)的图象上,直线  经过点
经过点  ,与
,与  轴交于点
轴交于点  ,连接
,连接  ,
,  .
. 
-
(1) 求
 ,
,  的值;
的值;
-
(2) 求
 的面积.
的面积.
在下列说法中,正确的是( )。
A . 合数都是偶数
B . 2的倍数都是合数
C . 2的倍数都是偶数
D . 5的倍数都是奇数
点P(﹣a2﹣1,a2+6)在第象限.
钟表在4点半时,它的时针与分针所成锐角是度.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径.若 , 弦
, 弦 , 则
, 则 的值为( )
的值为( )
 , 弦
, 弦 , 则
, 则 的值为( )
的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
不等式组  的解集.
的解集.
 的解集.
的解集.
在平面直角坐标系内,下列说法错误的是( )
A . 原点O不在任何象限内
B . 原点O的坐标是0
C . 原点O既在x轴上也在y轴上
D . 原点O在坐标平面内
如图,  是正八边形
是正八边形  的外接圆,则下列四个结论中正确的是( )
的外接圆,则下列四个结论中正确的是( )
 是正八边形
是正八边形  的外接圆,则下列四个结论中正确的是( )
的外接圆,则下列四个结论中正确的是( ) 
A .  的度数为
的度数为  B .
B .  C .
C .  为等边三角形
D .
为等边三角形
D . 
 的度数为
的度数为  B .
B .  C .
C .  为等边三角形
D .
为等边三角形
D . 
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2等于度.

如图,从一块半径为  的圆形铁皮上剪出一个圆心角是
的圆形铁皮上剪出一个圆心角是  的扇形
的扇形  ,则此扇形围成的圆锥底面圆的半径为( )
,则此扇形围成的圆锥底面圆的半径为( )
 的圆形铁皮上剪出一个圆心角是
的圆形铁皮上剪出一个圆心角是  的扇形
的扇形  ,则此扇形围成的圆锥底面圆的半径为( )
,则此扇形围成的圆锥底面圆的半径为( ) 
A . 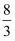 B .
B .  C .
C .  D .
D . 
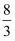 B .
B .  C .
C .  D .
D . 
如图,已知直线y1=ax+b与y2=mx+n相交于点A(2,﹣1),若y1>y2 , 则x的取值范围是( )

A . x<2
B . x>2
C . x<﹣1
D . x>﹣1
我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是  尺.根据题意,可列方程为( )
尺.根据题意,可列方程为( )
 尺.根据题意,可列方程为( )
尺.根据题意,可列方程为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图 ,△ABC 中,DE // AB 交 AC 于 D , 交 BC 于 E , 若 AD=2,CD=3,DE=4,则 AB =( )

A . 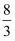 B .
B . 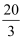 C .
C . 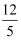 D . 6
D . 6
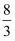 B .
B . 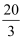 C .
C . 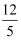 D . 6
D . 6
与![]() 相乘,结果是1的数为( )
相乘,结果是1的数为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
如图,PB、PC分别是△ABC的外角平分线,它们相交于点P,求证:点P在∠A的平分线上.

下列命题是真命题的是( )
A .菱形的对角线相等 B .直角三角形斜边上的中线等于斜边的一半
C .圆内接四边形对角相等 D .三角形的内心是三角形三条边的垂直平分线的交点
如图,点E(0,3),O(0,0),C(4,0)在⊙A上,BE是⊙A上的一条弦.则sin∠OBE=
.
![]()

最近更新
- 有人认为CH2=CH2与Br2的加成反应,实质是Br2先断裂为Br+和Br—,然后Br+首先与CH2=CH2一端碳原子结
- 下图为珠江三角洲地区产业结构变化和工业总产值增长图,读图完成25~27题。25.下列有关珠江三角洲地区产业结构从1980
- 读图,完成下列各题(阴影部分为黑夜)。(1)该图是以__________极点为中心的示意图,P点在N点的________
- Emma looked after her pet dog________ of all herfriends. A.c
- 五行学说不仅认为世界的本原就是木、火、土、金、水五种具体的物质形态,还以五行之间的生克关系来阐释事物之间的制约关系,认为
- OA杆是机器带动绕其轴线旋转的竖直杆,细绳的一端固定在杆的A点,另一端系一质量m=1 kg的小球,绳长为L=1 m.开始
- 下列微生物中能使面包变得蓬松可口的是 A.④ B.③ C.②
- 选出没有错别字的一项( ) A.怙恶不悛 合盘托出 和衷共济 讳莫如深 B.幡然悔悟 利令至昏 迷天大谎 一蹶不振
- (2013山东青岛二中检测)下列有关热力学第二定律的说法正确的是( ) A.气体自发地扩散运动总是向着
- 如图所示,在空间四边形ABCD中,AB=BC,CD=DA,E、F、G分别为CD、DA和AC的中点.求证:平面BEF⊥平面
- (11·孝感)如图,直线AB、CD交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT等于(
- —Are you in grade? —Yes, we are. A:different
- 8欧盟建立的背景是 A.经济全球化的过程中各国之间的经济竞争日益加剧 B.世界各国经济联系加强且相互间消除了贸易障碍 C
- 如图,正方形ABCD的边长为2,过点A作AE⊥AC,AE=1,连接BE,则tanE=_____________.
- 下列图象与对应的叙述相符合的是( ▲ ) A.等质量的铁片、铝片分别与足量且质量分数相同的稀硫酸反应 B.向H2SO4和
- 左下图为某流域20世纪50年代以来的气候要素变化图,右下图为气候变化对该流域农业生产的影响图,读图回答20~21题。20
- 关于遥感技术的叙述,正确的是 A.遥感是人们利用肉眼在遥远的宇宙空间对地面事物进行感知 B.遥感是人们利用一定技术装备,
- 在光滑的绝缘水平面上,有一个正三角形abc,顶点a、b、c处分别固定一个正点电荷,电荷量相等,如图所示,D点为正三角形外
- (本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分. 已知椭圆,常数、,且. (1
- 2009年3月10日,财政部发布公告,决定发行2009年凭证式(一期)国债300亿元。公告显示,本期国债发行期为2009



