初中 数学
若整数  使关于
使关于  的分式方程
的分式方程 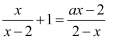 有整数解,使关于y的不等式组
有整数解,使关于y的不等式组  有且仅有四个整数解,则符合条件的所有整数a之积为( )
有且仅有四个整数解,则符合条件的所有整数a之积为( )
 使关于
使关于  的分式方程
的分式方程 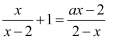 有整数解,使关于y的不等式组
有整数解,使关于y的不等式组  有且仅有四个整数解,则符合条件的所有整数a之积为( )
有且仅有四个整数解,则符合条件的所有整数a之积为( )
A . 2
B . -6
C . 6
D . -18
已知二次函数的解析式为y=ax2+bx+c(a、b、c为常数,a≠0),且a2+ab+ac<0,下列说法:
①b2﹣4ac<0;
②ab+ac<0;
③方程ax2+bx+c=0有两个不同根x1、x2 , 且(x1﹣1)(1﹣x2)>0;
④二次函数的图象与坐标轴有三个不同交点,
其中正确的个数是( )
A . 1
B . 2
C . 3
D . 4
若  ,则x-2y+z=.
,则x-2y+z=.
 ,则x-2y+z=.
,则x-2y+z=.
等腰三角形的两条边长分别为2 和5
和5 , 那么这个三角形的周长等于 .
, 那么这个三角形的周长等于 .
 和5
和5 , 那么这个三角形的周长等于 .
, 那么这个三角形的周长等于 .
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点三角形△ABC(即三角形的顶点都在格点上).

-
(1) 在图中作出△ABC关于直线MN的对称图形△A′B′C′.
-
(2) 利用网格纸,在MN上找一点P,使得PB+PC的距离最短.(保留痕迹)
如图,⊙O与直线  相离,圆心
相离,圆心  到直线
到直线  的距离
的距离  ,
,  ,将直线
,将直线  绕点
绕点  逆时针旋转
逆时针旋转  后得到的直线
后得到的直线  刚好与⊙O相切于点
刚好与⊙O相切于点  ,则⊙O的半径= .
,则⊙O的半径= .
 相离,圆心
相离,圆心  到直线
到直线  的距离
的距离  ,
,  ,将直线
,将直线  绕点
绕点  逆时针旋转
逆时针旋转  后得到的直线
后得到的直线  刚好与⊙O相切于点
刚好与⊙O相切于点  ,则⊙O的半径= .
,则⊙O的半径= .
下列方程组中,属于二元二次方程组的为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知两点A(3,2)和B(1,-2),点P在y轴上且使AP+BP最短,则点P的坐标是( ).
A . (0,  )
B . (0,
)
B . (0,  )
C . (0,-1)
D . (0,
)
C . (0,-1)
D . (0,  )
)
两个连续奇数的平方差是( )
A . 16的倍数
B . 8的倍数
C . 12的倍数
D . 6的倍数
已知一组数据5,4,x,3,9的平均数为5,则x的值是。
如图,  .若
.若  ,
,  ,则
,则  .
.
 .若
.若  ,
,  ,则
,则  .
. 
如图所示,直线a、b被直线c所截,∠1与∠2是( )

A . 内错角
B . 同位角
C . 同旁内角
D . 邻补角
某商品涨价30%后欲恢复原价,则必须下降的百分数约为( )
A . 20%
B . 21%
C . 22%
D . 23%
若  ,则a的取值范围是( )
,则a的取值范围是( )
 ,则a的取值范围是( )
,则a的取值范围是( )
A . a为正数
B . a为负数
C . a为非负数
D . a为非正数
如图,点D在△ABC中,∠BDC=90°,AB=6,AC=BD=4,CD=2,则图中阴影部分的面积为.

某河受暴雨袭击,某天此河水的水位记录如下表:
| 时间(时) | 0 | 4 | 8 | 12 | 16 | 20 | 24 |
| 水位(米) | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 |
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多高?
(3)哪一时段水位上升最快?
计算:若5x+19的立方根是4,求2x+18的平方根.
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位![]() :个)
:个)
| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲班 | 100 | 98 | 110 | 90 | 102 |
| 乙班 | 90 | 100 | 95 | 120 | 95 |
请解答下列问题
⑴计算两个班这五名学生的优秀率。
⑵通过计算说明,哪个班的比赛成绩稳定?
⑶通过上面的计算你认为应该定哪一个班为冠军更![]() 合适?请说明你的
合适?请说明你的![]() 理由。
理由。
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距离A地18km 的B地,他们离出发地的距离S(km)和行驶时间t(h)之间的函数关系的图象如图所示.根据图中提供的信息,符合图象描述的说法是( )
A. 甲在行驶的过程中休息了一会 B.乙在行驶的过程中没有追上甲
C. 乙比甲先到了B地 D. 甲的行驶速度比乙的行驶速度大

如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=6 cm,则线段PB的长度为 cm.
 |
最近更新
- 果蝇的红眼和白眼是性染色体上的一对等位基因控制的相对性状。用一对红眼雌雄果蝇交配,子一代中出现白眼果蝇。让子一代果蝇自由
- 若,则下列函数:①,②,③,④中,随的增大而增大的函数有( ▲ )A.①②③ B
- 下列变化中,分子种类发生了改变的是 A.水结成冰 B.氧气液化 C.干冰升华
- David has won the first prize in singing; he is still very e
- 春天来了,某池塘中的荷花枝繁叶茂,已知每一天荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶覆盖
- 财政部、国家税务总局宣布,从2008年9月1日起调整汽车消费税,大幅度提高3.0升以上大排量、高油耗乘用车的消费税税率,
- 作文 茫茫历史长河中,谁是英雄?是在兵临城下之际,不计个人恩怨以老迈之躯夜缒出城屈人之兵的烛之武,还是在强秦铁蹄踏碎中原
- 如图7将冰放入水壶,然后不断加热,观察到冰 成水,水蒸气遇到冷的钢勺又 成水(填写物态变化名称)。
- 四川灾后重建中,在某工地上一卡车以速度10m/s匀速行驶,刹车后第1个2s内位移与最后一个2s内位移之比为3∶2,设卡车
- 函数的图象是一条过原点(0,0)及点(2, )的直线.
- “A house divided(分裂、裂开)against itself can not stand.”这句名言出自美
- 4.在下面一段文字横线处填入语句,衔接最恰当的一项是( ) 近代以来,中国的现代科学和高等教育事业由于起步晚、底子薄,
- 商场某品牌的手机进价是2 400元,春节期间商场准备搞促销活动,计划按标价的八折出售,这样商场仍可获利10%,小明在促销
- She got stuckin a terrible traffic jam on the highway to Gu
- 下列各组中属于相对性状的是 A. 玉米的黄粒和圆粒 B.家鸡的长腿和毛腿 C.绵羊的白毛和黒毛
- 据报道,最近我国科学家使用被称为“人造太阳”的中国环流器二号A实验装置,使其内部等离子体温度“跃升”到5500万摄氏度,
- Thecollege________7 departments,4 institutes,and Teaching D
- 有关氮气说法错误的是A .氮气还能用于灯泡填充气B .通常情况下氮气的化学性质很活泼C .氮气不能供给呼吸D .高浓度氮
- 阅读下面的材料,然后按要求作文。 “加油!”简单的一句话,让她浑身充满了力量,顽强地冲向终点。“孩子,老师说你做得不错,
- 某地一辆满载浓硫酸的罐车翻倒,导致溶质质量分数为98%的浓硫酸20t泄漏,并向路基两边蔓延。接到报警后消防官兵立即赶来并



