初中 数学

-
(1) 计算:
 ;
;
-
(2) 解不等式组:
 ,并写出它的正整数解.
,并写出它的正整数解.


-
(1) 试猜想DM与ME的数量关系,并证明你的结论.
-
(2) 拓展与延伸:
①若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为;
②如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,猜想并证明DM和ME的关系.下面给出部分证明过程,请把推理过程补充完整.
证明: 如图③,连结AC.
∵四边形ABCD、四边形ECGF都是正方形,
∴∠DAC=∠DCA=∠DCE=∠CFE=45°,
∴点E在AC上.
∴∠AEF=∠FEC=90°.
又∵点M是AF的中点,
∴ME=
 AF.
AF.
 .则AC的长为.
.则AC的长为.
 的值为6,则
的值为6,则  的值为( )
的值为( )
 有意义,则实数x的取值范围是.
有意义,则实数x的取值范围是.
-
(1) 已知(x﹣1)2=4,求x的值;
-
(2)

 ×
×  =;12÷
=;12÷  =.
=.
-
(1) 8x=-2(x+4)
-
(2)
 =3-
=3-  .
.

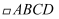 中,
中,  平分
平分  ,交
,交  于点
于点  ,
, 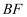 平分
平分 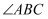 ,交
,交  于点
于点  .
.  与
与 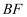 交于点
交于点  ,连接
,连接  ,
,  .
. 
-
(1) 求证:四边形
 是菱形;
是菱形;
-
(2) 若
 ,
,  ,
,  ,求
,求  的度数.
的度数.
如图,阴影部分面积是 。

A种饮料比![]() 种饮料单价少1元,小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元,如果设B种饮料单价为
种饮料单价少1元,小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元,如果设B种饮料单价为![]() 元/瓶,那么下面所列方程正确的是
元/瓶,那么下面所列方程正确的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
如图,将一张边长为6的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,则剩余部分的面积为( )
A.36 B. ![]() C.
C.![]() D.
D.![]()

如图,饮水桶中的水由图![]() 的位置下降到图
的位置下降到图![]() 的位置的过程中,如果水减少的体积是
的位置的过程中,如果水减少的体积是![]() ,水位下降的高度是
,水位下降的高度是![]() ,那么能够表示
,那么能够表示![]() 与
与![]() 之间函数关系的图象是
之间函数关系的图象是
 |  |  |  | ||||||
 | |||||||||
![]()
![]()
A B C D
将2.95用四舍五入法精确到十分位,其近似值为 .
.如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是
A.∠2=∠1,∠B=∠D B.AB=AD,∠3=∠4
C.∠2=∠1,∠3=∠4 D.AB=AD,∠2=∠1
- 从以下各句中找出没有语病的一句( ) A、鼓乐喧天,红旗招展,游行队伍在欢快地行进着。 B、夏天放暑假时我也没有回家,为
- 下列反应中,属于加成反应的是( )A.乙烯使KMnO4酸性溶液褪色B.将苯滴入溴水中,振荡后水层接近无色C.乙烯使
- 江苏省消费者协会公布了对于消费行为的调查结果,发现人们在日常消费中仍比较普遍地存在着下列消费行为:购物跟着“打折”走,买
- the day went on, the weather got worse. A.With
- 关于乙醇结构的说法中正确的是A.乙醇中有-OH,所以乙醇溶解于水,可以电离出OH-而显碱性B.乙醇与乙酸反应生成乙酸乙酯
- 下列气体中的主要成分不是甲烷的是( )A.沼气 B.天然气
- 目前有一种磁强计,用于测定地磁场的磁感应强度.磁强计的原理如右图所示,电路有一段金属导体,它的横截面是宽为a、高为b的长
- 下表是人体成熟红细胞与血浆中的K+和Mg2+在不同条件下的含量比较,不正确的是()处理前 用鱼滕酮处理后 用乌苯苷处理
- 补写出下列名篇名句中的空缺部分。 (1)登高而招,__________,而见者远;顺风而呼,__________,而闻者
- 比较下列加线词的意义和用法,判断正确的一项是 ①奉宣室以何年 ③ 老当益壮 ② 处涸辙
- 方程表示圆心为的圆,则圆的半径( ) A. B. C.
- 设NA表示阿伏加德罗常数的数值,下列叙述正确的是() A.常温常压下,2.8 g N2与C2H4的混合气体中含有的电子数
- 14.下列各句中,没有语病的一句是(3分) A.过多地介入孩子的生活,无论是由于爱护还是由于焦虑,都是在培养孩子依
- 下列词语中没有错别字的一项是( ) A.油光可签 抑扬顿措 宽恕 文绉绉 B.奥密 幽默
- 2008年北京奥运体操全能比赛是按照“自、鞍、吊、跳、双、单”的顺序进行,单杠列为全能比赛的最后一项.号称“世界体操全能
- 如图,在平面直角坐标系中,直线y=x与双曲线y=(k≠0)交于点A,过点C(0,2)作AO的平行线交双曲线于点B,连接A
- 纤维素分解菌的选择培养基有选择作用,原因在于() A.NaNO3 B.KCl C
- —What made her struggle ________ an artist so hard?( ) —___
- We will soon discuss the problem ______we should take some e
- 不等式≥2的解集为………………………()A.[-1,0)



