初中 数学
满足不等式x-1≤3的自然数是( )
A . 1,2,3,4
B . 0,1,2,3,4
C . 0,1,2,3
D . 无穷多个
数轴上表示整数的点称为整点.某数轴的单位长度是1 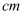 ,若在这个数轴上随意画出一条长为2020
,若在这个数轴上随意画出一条长为2020 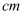 的线段
的线段  ,则线段
,则线段  盖住的整点个数是( )
盖住的整点个数是( )
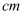 ,若在这个数轴上随意画出一条长为2020
,若在这个数轴上随意画出一条长为2020 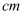 的线段
的线段  ,则线段
,则线段  盖住的整点个数是( )
盖住的整点个数是( )
A . 2018或2019
B . 2019或2020
C . 2020或2021
D . 2021或2022
彼此相似的矩形  ,
,  ,
,  ,…,按如图所示的方式放置.点
,…,按如图所示的方式放置.点  ,
,  ,
,  ,…,和点
,…,和点  ,
,  ,
,  ,…,分别在直线y=kx+b(k>0)和x轴上,已知点
,…,分别在直线y=kx+b(k>0)和x轴上,已知点 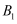 、
、  的坐标分别为(1,2),(3,4),则
的坐标分别为(1,2),(3,4),则  的坐标是( ).
的坐标是( ).
 ,
,  ,
,  ,…,按如图所示的方式放置.点
,…,按如图所示的方式放置.点  ,
,  ,
,  ,…,和点
,…,和点  ,
,  ,
,  ,…,分别在直线y=kx+b(k>0)和x轴上,已知点
,…,分别在直线y=kx+b(k>0)和x轴上,已知点 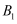 、
、  的坐标分别为(1,2),(3,4),则
的坐标分别为(1,2),(3,4),则  的坐标是( ).
的坐标是( ).
A . (  ,
,  )
B . (
)
B . (  -
-  ,
,  )
C . (
)
C . (  -
-  ,
,  )
D . (
)
D . (  -1,
-1,  )
)
 ,
,  )
B . (
)
B . (  -
-  ,
,  )
C . (
)
C . (  -
-  ,
,  )
D . (
)
D . (  -1,
-1,  )
)
比较大小: 
 ( 填 >、< 或 = )。
( 填 >、< 或 = )。

 ( 填 >、< 或 = )。
( 填 >、< 或 = )。
18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,

解答下列问题:

解答下列问题:
-
(1) 根据上面多面体模型,完成表格中的空格,你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是.
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
12
正八面体
8
12
正十二面体
20
12
30
…
-
(2) 一个多面体的面数与顶点数相等,有12条棱,这个多面体是面体.
将抛物线y=﹣2x2+1向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为.
如图,已知直线l1∥l2 , 将等边三角形如图放置,若∠β=20°,则∠α等于.

某商场四月份的营业额是200万元,如果该商场第二季度每个月营业额的增长率相同,都为  ,六月份的营业额为
,六月份的营业额为  万元,那么
万元,那么  关于
关于  的函数解式是.
的函数解式是.
 ,六月份的营业额为
,六月份的营业额为  万元,那么
万元,那么  关于
关于  的函数解式是.
的函数解式是.
正比例函数y=mx和反比例函数  的一个交点为(1,2),则另一个交点是.
的一个交点为(1,2),则另一个交点是.
 的一个交点为(1,2),则另一个交点是.
的一个交点为(1,2),则另一个交点是.
计算:  =
=
 =
=
如图,在菱形ABCD中,对角线AC,BD相交于点O,H为BC中点,AC=6,OH= . 则线段BD的长为( )
. 则线段BD的长为( )
 . 则线段BD的长为( )
. 则线段BD的长为( )
A . 8
B . 5
C . 4
D . 

如图,把  沿
沿  翻折,点
翻折,点  落在点
落在点  的位置,若
的位置,若  ,则
,则  的大小为.
的大小为.
 沿
沿  翻折,点
翻折,点  落在点
落在点  的位置,若
的位置,若  ,则
,则  的大小为.
的大小为. 
如图,已知△CAB,∠ACB=90°.

-
(1) 请用直尺和圆规过点C作一条裁剪线,使其将△ABC分成两个相似的三角形.(保留作图痕迹,不写作法)
-
(2) 若CA=3,CB=4,则(1)中作的裁剪线的长为.
写出一个解为1和2的一元二次方程:.
位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,  ≈1.41).
≈1.41).
 ≈1.41).
≈1.41). 
已知:四边形ABCD是正方形,E是AB边上一点,F是BC延长线上一点,且DE=DF.

-
(1) 如图1,求证:DF⊥DE;
-
(2) 如图2,连接AC,EF交于点M,求证:M是EF的中点.
如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第n个图案有 个三角形(用含n的代数式表示)

因式分解
![]()
解方程组 并求
并求![]() 的值.
的值.
如图,点A是反比例函数y=![]() 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )

A.3 B.﹣3 C.6 D.﹣6
最近更新
- 根据句意,从方框中选择恰当的单词或短语填空。allow, too many, wrong,guess, work ou
- 如图,有一半径为R的半圆形曲面MPQ,质量为2m的A球与质量为m的B球, 用轻质绳连接后挂在圆柱曲面边缘.现将A球从边缘
- It is high time for us to take measures to protect these old
- 下列各句中,没有语病的一句是 () A.为了总结开展“研究性学
- 圣琵琶传闻 有书生欲游吴地,道经江西,因风阻泊船,闲步入林,过①一僧院。僧已他出,房门外,小廊数间,傍有笔砚。书生攻②画
- I wonder _________Eddie has gone to Singapore.A.how longB.ho
- 我国对可呼吸的钠-二氧化碳电池的研究取得突破性进展,该电池的总反应式为: 4Na+3CO22Na2CO3+C,其工作原理
- 下列关于蛋白质和氨基酸的叙述,正确的是() A.具有生物催化作用的酶都是由氨基酸组成的 B.高等动物能合成生命活动所需的
- 14.阅读下面这首词,完成题目。 南柯子·忆旧 仲 殊 十里青山远,潮平路带沙。数声啼鸟怨年华,又是凄凉时候在天涯。
- 依次填入下面一段文字横线处的语句,与上下文衔接最恰当的一组是 发射窗口定在凌晨。___________。火箭______
- (2009.海南月考)下列有关村民自治的观点中,正确的是
- 新发明改变了我们的生活,同时出现了很多新的职业,下列职业按出现先后排序正确的是 A、电话接线员—火车司机—空姐—
- “中国制造”在国际市场上素以“物美价廉”著称。但现在,低价鞋给贸易保护主义者以口实,国外反倾销已成为我国鞋类出口的极大障
- 下列属于健康状态的是( )A.精力旺盛,一天只睡2—3小时即可 B.没病没灾C.吃得饱,睡得好 D.身体健康
- 在空间直角坐标系中,点A(﹣1,2,0)和点B(3,﹣2,2)的距离为
- 9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的抽取方法是(
- 下列说法中正确的是:A.物体吸收热量,其内能必增加B.外界对物体做功,物体内能必增加C.物体吸收热量,同时对外做功,其内
- The boy seized a stick and ___ the dog, but it ran away. A.
- 求函数在区间上的最大值与最小值。
- 酸雨给人类生活和社会发展带来了严重危害。汽车尾气是导致酸雨的重要原因,为减少有害气体的排放,人们在汽车排气管上安装“催化



