初中数学：七年级　 八年级　 九年级　 中考　

初中数学

解方程：x（x－1）＝3（x－1）

图（1）是一个横断面为抛物线形状的拱桥，当水面在图（1）位置时，拱顶（拱桥洞的最高点）离水面2 m，水面宽4 m.如图（2）建立平面直角坐标系，则抛物线的关系式是（）

图片_x0020_1927927553

A . y=﹣2x² B . y=2x² C . y=﹣0.5x² D . y=0.5x²

如图所示，在△ABC中，∠B＝90°，AB＝BC＝4，D，E，F分别是AC，BC，AB边上的点，且∠EDF＝45°，DE＝DF，则AF+CE＝.

如图，AB=2，BC=5，AB⊥BC于B，l⊥BC于C，点P自点B开始沿射线BC移动，过点P作PQ⊥PA交直线l于点Q．

下面说法中，正确的是（）

A . 实数分为正实数和负实数 B . 带根号的数都是无理数 C . 无限不循环小数都是无理数 D . 平方根等于本身的数是1和0

如图，在下列图形中，最具有稳定性的是（）

A .

B .

C .

D .

如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD于点E，AD平分∠BDE.

下列各式中，从左到右变形正确的是（）

A . $\text{[math]}$ ＝a+b B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

如图，在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE．

用反证法证明“a<0”时，应先假设（）

A . a>0 B . a=0 C . a $\text{[math]}$ 0 D . a不为0

如图，已知抛物线y=ax²+bx+c（a≠0）经过A（3，0），B（﹣5，0），C（0，﹣5）三点，O为坐标原点.

（1）求此抛物线的解析式；
（2）把抛物线y=ax²+bx+c（a≠0）向上平移 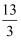$\text{[math]}$ 个单位长度，再向左平移n（n＞0）个单位长度得到新抛物线，若新抛物线的顶点M在△ABC内，求n的取值范围；
（3）设点P在y轴上，且满足∠OPA+∠OCA=∠CBA，求CP的长.

计算 $\text{[math]}$ 的结果是（）

A . 5 B . －5 C . 1 D . －1

某校为创建书香校园，开展了师生“大阅读”活动，并制定“大阅读”星级评选方案（以整数评分），每月评选一次，为了解活动开展情况，某星期学校对全校七年级“大阅读”星级评选作进行抽样调查，随机抽取20名学生阅读的积分情况进行分析．

20名学生的“大阅读”积分如下（单位：分）：

32 43 34 35 15 46 48 24 45 10

25 40 60 42 55 30 47 28 37 42

按如下表格分组整理、描述样本数据．

根据以上数据制成如下不完整的频数分布直方图．

（1）填空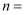： $\text{[math]}$ ， $\text{[math]}$ ；并补全频数分布直方图；
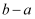（2）已知该校七年级学生小林的积分为 $\text{[math]}$ 分，是绿星级；小乐的积分为 $\text{[math]}$ ，是青星级．如果两人的积分均未出现在样本中，求 $\text{[math]}$ 的最大值．

已知多项式（2x²+ax﹣y+6）﹣（2bx²﹣3x+5y﹣1）．

（1）若多项式的值与字母x的取值无关，求a、b的值．
（2）在（1）的条件下，先化简多项式3（a²﹣ab+b²）﹣（3a²+ab+b²），再求它的值．
（3）在（1）的条件下，求（b+a²）+（2b+ $\text{[math]}$ a²）+（3b+ $\text{[math]}$ a²）+…+（9b+ $\text{[math]}$ a²）的值．