初中 数学
A、B两地果园分别有橘子40吨和60吨,C、D两地分别需要橘子30吨和70吨;已知从A、B到C、D的运价如表:
|
到C地 |
到D地 |
|
|
A果园 |
每吨15元 |
每吨12元 |
|
B果园 |
每吨10元 |
每吨9元 |
-
(1) 若从A果园运到C地的橘子为x吨,则从A果园运到D地的橘子为吨,从A果园将橘子运往D地的运输费用为元;
-
(2) 设总运费为y元,请你求出y关于
 的函数关系式;
的函数关系式;
-
(3) 求总运输费用的最大值和最小值;
-
(4) 若这批橘子在C地和D地进行再加工,经测算,全部橘子加工完毕后总成本为w元,且w=-(x-25)2+4360,则当x= 时,w有最 值(填“大”或“小”).这个值是 .
为庆祝中国 百年华诞,某校德育处组织开展以“红色经典伴我成长”为主题的系列教育活动.学校要求每名同学至少购买革命红书1册并进行阅读.小敏调查了班级里40名同学本学期购买革命红书册数的情况,并将结果绘制成如下统计图.请根据图中信息,解答下列问题.
百年华诞,某校德育处组织开展以“红色经典伴我成长”为主题的系列教育活动.学校要求每名同学至少购买革命红书1册并进行阅读.小敏调查了班级里40名同学本学期购买革命红书册数的情况,并将结果绘制成如下统计图.请根据图中信息,解答下列问题.
 百年华诞,某校德育处组织开展以“红色经典伴我成长”为主题的系列教育活动.学校要求每名同学至少购买革命红书1册并进行阅读.小敏调查了班级里40名同学本学期购买革命红书册数的情况,并将结果绘制成如下统计图.请根据图中信息,解答下列问题.
百年华诞,某校德育处组织开展以“红色经典伴我成长”为主题的系列教育活动.学校要求每名同学至少购买革命红书1册并进行阅读.小敏调查了班级里40名同学本学期购买革命红书册数的情况,并将结果绘制成如下统计图.请根据图中信息,解答下列问题.

-
(1) 这次调查获取的样本数据的众数是;中位数是.
-
(2) 该校共有学生1200人,根据样本数据,估计本学期学生购买革命红书4册及以上的学生共有多少人.
8:15比的前项扩大3倍,要使比值不变,比的后项也应该扩大倍.
计算:  。
。
 。
。
如图,在  中,A,B两点在
中,A,B两点在  轴上方,以点
轴上方,以点  为位似中心,在
为位似中心,在  轴的下方作
轴的下方作  的位似图形
的位似图形  ,把
,把  的边长放大到原来的2倍,设点
的边长放大到原来的2倍,设点  的对应点
的对应点  的坐标是
的坐标是  ,则点
,则点  的坐标是( )
的坐标是( )
 中,A,B两点在
中,A,B两点在  轴上方,以点
轴上方,以点  为位似中心,在
为位似中心,在  轴的下方作
轴的下方作  的位似图形
的位似图形  ,把
,把  的边长放大到原来的2倍,设点
的边长放大到原来的2倍,设点  的对应点
的对应点  的坐标是
的坐标是  ,则点
,则点  的坐标是( )
的坐标是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列说法中正确的个数为( )
⑴正数与负数互为相反数;⑵单项式  的系数是3,次数是2;
的系数是3,次数是2;
⑶如果  ,那么
,那么  ;⑷过两点有且只有一条直线;
;⑷过两点有且只有一条直线;
⑸一个数和它的相反数可能相等;⑹射线比直线小一半.
A . 1个
B . 2个
C . 3个
D . 4个
如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为 .
把多项式2m2﹣4m4+2m﹣1按m的升幂排列.
如图,CD是经过∠BCA顶点C的一条直线,且直线CD经过∠BCA的内部,点E,F在射线CD上,已知CA=CB且∠BEC=∠CFA=∠α.

-
(1) 如图1,若∠BCA=80°,∠α=90°,问EF=BE-AF,成立吗?说明理由.
-
(2) 将(1)中的已知条件改成∠BCA=∠β,∠α+∠β=180°(如图2),问EF=BE-AF仍成立吗?说明理由.
小明根据学习函数的经验,对函数y= +1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
+1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
 +1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
+1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:

-
(1) 函数y=
 +1的自变量x的取值范围是;
+1的自变量x的取值范围是;
-
(2) 如表列出了y与x的几组对应值,请写出m,n的值:m=,n=;
x
…
﹣
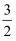
﹣1
﹣

0

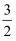
2

3

…
y
…

m

0
﹣1
n
2

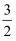

…
-
(3) 在如图所示的平面直角坐标系中,描全上表中以各对对应值为坐标的点,并画出该函数的图象.
-
(4) 结合函数的图象,解决问题:
①写出该函数的一条性质:.
②当函数值
 +1>
+1>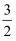 时,x的取值范围是:.
时,x的取值范围是:.
下列各数:-3.6,-0.5, 0.2,  , 0,19,-72, 12%,其中负数有( )
, 0,19,-72, 12%,其中负数有( )
 , 0,19,-72, 12%,其中负数有( )
, 0,19,-72, 12%,其中负数有( )
A . 2 个
B . 3 个
C . 4 个
D . 5 个
(﹣2)2019+(﹣2)2020等于( )
A . ﹣22019
B . ﹣22020
C . 22019
D . ﹣2
△ABC在直角坐标系中如图摆放,其中顶点A,B,C的坐标分别为(﹣4,1),(﹣1,﹣1),(﹣3,2),若将△ABC绕点B顺时针方向旋转90°,则A点的对应点的坐标为 .

下列说法错误的是( )
A . 有两边相等的三角形是等腰三角形
B . 直角三角形不可能是等腰三角形
C . 有两个角为60°的三角形是等边三角形
D . 有一个角为60°的等腰三角形是等边三角形
某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A . 50(1+x)2=182
B . 50+50(1+x)+50(1+x)2=182
C . 50(1+2x)=182
D . 50+50(1+x)+50(1+2x)2=182
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是多少?

民族要复兴,乡村必振兴2月21日发布的2021年中央一号文件,主题是全面推进乡村振兴加快农业农村现代化.乡村振兴战略的实施效果要用农民生活富裕水平来评价,某合作社为尽快打开市场,对本地新产品进行线上和线下销售相结合的模式,具体费用标准如下:
线下销售模式:标价5元/千克,八折出售;
线上销售模式:标价5元/千克,九折出售,超过6千克时,超出部分每千克再让利1.5元.
购买这种新产品x千克,所需费用为y元,y与x之间的函数关系如图所示.

根据以上信息回答下列问题:
-
(1) 请求出两种销售模式对应的函数解析式;
-
(2) 说明图中点C坐标的实际意义;
-
(3) 若想购买这种产品10千克,请问选择哪种模式购买最省钱?
当 时,分式 有意义.
有意义.
 有意义.
有意义.
已知,如图1,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)求证:△BCE≌△DCF;
(2)求CF的长;
(3)如图2,在AB上取一点H,且BH=CF,若以BC为x轴,AB为y轴建立直角坐标系,问在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的P点坐标;若不存在,说明理由.


在2017年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数、中位数、方差依次为( )
| 成绩/分 | 27 | 28 | 30 |
| 人数 | 2 | 3 | 1 |
A.28,28,1 B.28,27.5,1 C.3,2.5,5 D.3,2,5
最近更新
- 已知:2CO(g)+O2(g)=2CO2(g)ΔH=-566 kJ/mol; Na2O2(s)+CO(g)=Na2CO3
- 下列口号属于五四运动的是A.“师夷长技以制夷” B.“民主、科学”C.“救
- 一定温度下,下列溶液的离子浓度关系式正确的是()A.0.1mol•L-1NaHCO3溶液中:C(Na+)+C(H+)=C
- 某展览厅内要用相同的正方体木块搭成一个三视图如下的展台,则此展台共需这样的正方体 (
- 假定英语课上老师要求同桌之间交换修改作文,请你修改你同桌写的以下作文。文中共有10处语言错误,每句中最多有两处。错
- 下列词语中没有错别字的一组是 A.暮霭 脱颖而出 精兵减政 口慧而实不至 B.安详 名门望族 矢志不渝 道不
- 在t ℃时,将a g NH3完全溶于水,得到V mL溶液,假设该溶液的密度为ρ g·mL-1,溶质的质量分数为w,其中含
- 以“创造思维“开头,重组下面语句,要求不改变原意。只有善于捕捉并反思生活中出现的重大问题,而且把它们上升到理论的高度上,
- . ________ I admit that there are problems, I don’t agree th
- 用四氯化碳萃取碘水中的碘,下列说法中不正确的是: A.实验使用的主要仪器是分液漏斗 B.碘在四氯化碳中的溶解
- 【甲】 记承天寺夜游 苏轼 元丰六年十月十二日夜,解衣欲睡,月色入户,欣然起行。念无与为乐者,遂至承天寺寻张怀民
- 下列词语中加点的字,每对读音都不相同的一项是 A.贩卖/皈依 靓妆/痉挛 雇佣/佣金 宁愿/息事宁人 B.泥
- 某河流中五年前引进了一种外来植物(甲)。跟踪调查发现,五年来,该河流中甲种群密度逐年显著增加,土著食草鱼类和水草的种群密
- 中国人上到泰山顶上,想到的可能是杜甫的诗;德国人上到泰山顶上,想到的可能是贝多芬的交响乐。从中我们可以看出 ①文化对人的
- 臣密今年四十有四,祖母今年九十有六, , 。 ,
- (2013·福建漳州质检)孟德斯鸠说:“自由就是做法律所许可的一切事情的权利。”他主要强调
- 下列词语中加点的字,每对读音都不相同的一项是( ) A.强迫/倔强 剥削/生吞活剥 曲径通幽
- 图4-3-2是胡萝卜在不同的含氧情况下从硝酸钾溶液中吸收K+和NO的曲线。影响A、B两点和B、C两点吸收量不同的因素分别
- 我国有许多抒发爱国情怀的诗词格言,下列体 现这一风格的是( ) ①“天道酬勤” ②“天下兴亡,匹夫有责
- He found that complex problems, especially those _____ abst



