初中 数学
现将某校七年一班女生按照身高共分成三组,下表是这个班级女生的身高分组情况统计表,则在统计表中  的值是.
的值是.
 的值是.
的值是. | 第一组 | 第二组 | 第三组 | |
| 每个小组女生人数 | 9 | 8 | |
| 每个小组女生人数占 班级女生人数的百分比 | | | 15% |
在某次作业中有这样的一道题:如果代数式5a+3b的值为-4,那么代数式2(a+b)+4(2a+b)的值是多少?小明是这样来解的:原式=2a+2b+8a+4b=10a+6b,把式子5a+3b=-4两边同乘以2,得10a+6b=-8.仿照小明的解题方法,完成下面的问题:
-
(1) 如果
 +a=0,则2020-a-
+a=0,则2020-a-  =.
=.
-
(2) 已知a-b=-2,求3(a-b)-5a+5b+6的值.
-
(3) 已知
 +2ab=3,ab-
+2ab=3,ab-  =-4,求2
=-4,求2  +
+ 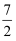 ab+
ab+  的值.
的值.
某年级举行篮球比赛,每一支球队都和其他球队进行了一场比赛,已知共举行了21场比赛,那么共有( )支球队参加了比赛.
A . 6
B . 12
C . 7
D . 14
如图,一次函数 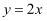 与反比例函数
与反比例函数  的图象交于点
的图象交于点  两点,点
两点,点  在以
在以  (-2,0)为圆心,1为半径的⊙
(-2,0)为圆心,1为半径的⊙  上,
上,  是
是  的中点,已知
的中点,已知  长的最大值为
长的最大值为  ,则
,则  的值为.
的值为.
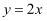 与反比例函数
与反比例函数  的图象交于点
的图象交于点  两点,点
两点,点  在以
在以  (-2,0)为圆心,1为半径的⊙
(-2,0)为圆心,1为半径的⊙  上,
上,  是
是  的中点,已知
的中点,已知  长的最大值为
长的最大值为  ,则
,则  的值为.
的值为. 
在九年级体育中考中,某校某班参加仰卧起坐测试的一组女生(每组6人)测试成绩如下(单位:次/分):44,42,48,46,47,45.则这组数据的极差为。
已知xn+1ym与﹣  x4y是同类项,则n=.
x4y是同类项,则n=.
 x4y是同类项,则n=.
x4y是同类项,则n=.
如果一个多边形的每个内角都相等,且内角和为1800度,那么这个多边形的一个外角是( )
A . 30°
B . 36°
C . 60°
D . 72°
若|x|=3,y2=4,且x>y , 则x﹣y=.
下列说法错误的是( )
A . 1的平方根是1
B . -1的立方根是-1
C .  是2的算术平方根
D . -4是
是2的算术平方根
D . -4是 的平方根
的平方根
 是2的算术平方根
D . -4是
是2的算术平方根
D . -4是 的平方根
的平方根
已知⊙O1的半径为3,⊙O2的半径为r,⊙O1与⊙O2只能画出两条不同的公共切线,且O1O2=5,则⊙O2的半径为r的取值范围是.
整理一批图书,由一个人做要40小时完成,现在计划先由x人做4小时后,再增加2人和他们一起8小时,共完成这项工作的  ,假设每个人的工作效率相同,则列方程正确的是( )
,假设每个人的工作效率相同,则列方程正确的是( )
 ,假设每个人的工作效率相同,则列方程正确的是( )
,假设每个人的工作效率相同,则列方程正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 是物理学中的一个公式,其中各个字母都不为零且
是物理学中的一个公式,其中各个字母都不为零且 . 用
. 用 表示R,则R=
表示R,则R=
如图,四边形ABCD中,  ,
,  ,
,  ,则BD的长为( )
,则BD的长为( )
 ,
,  ,
,  ,则BD的长为( )
,则BD的长为( ) 
A . 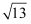 B . 5
C .
B . 5
C . 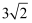 D .
D . 
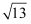 B . 5
C .
B . 5
C . 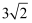 D .
D . 
某同学参加校艺术节独唱比赛,其中唱功、表情、动作三个方面得分分别为90分、80分、95分,综合成绩中唱功占70%,表情占10%,动作占20%,则该名同学综合成绩为分.
已知电压 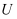 、电流
、电流 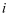 、电阻
、电阻  三者之间的关系为:
三者之间的关系为:  .当其中一个量是常量时,另外两个变量之间的图象不可能是( )
.当其中一个量是常量时,另外两个变量之间的图象不可能是( )
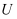 、电流
、电流 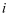 、电阻
、电阻  三者之间的关系为:
三者之间的关系为:  .当其中一个量是常量时,另外两个变量之间的图象不可能是( )
.当其中一个量是常量时,另外两个变量之间的图象不可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
(教材呈现)下图是华师版数学教材的部分内容

探索
如图24.2.1,画  ,并画出斜边
,并画出斜边  上的中线
上的中线  ,量一量,看看
,量一量,看看  与
与  有什么关系.
有什么关系.
相信你与你的伙伴一定会发现:  恰好是
恰好是  的一半,下面让我们演绎推理证明这一猜想.
的一半,下面让我们演绎推理证明这一猜想.
已知:如图24.2.2,在  ,
,  ,
,  是斜边
是斜边  上的中线.
上的中线.
求证:  .
.

-
(1) (证明)请根据教材图24.2.2的提示,完成直角三角形的性质“直角三角形斜边中线等于斜边一半”的证明
-
(2) (延伸)如图①,在四边形
 中,
中,  ,
,  ,点E、F分别为
,点E、F分别为  ,
,  的中点,连结
的中点,连结  、
、  ,则线段
,则线段  与
与  的数量关系是.
的数量关系是.
-
(3) (应用)
如图②,在(延伸)的条件下,当
 平分
平分  ,
,  时,则
时,则  的大小为 ▲ .
的大小为 ▲ .如图③,在(延伸)的条件下,当
 ,四边形
,四边形  是菱形时,直接写出四边形
是菱形时,直接写出四边形  的面积.
的面积.
如图,矩形  中,
中,  ,把矩形沿对角线
,把矩形沿对角线  所在直线折叠,使点
所在直线折叠,使点  落在点
落在点  处,
处,  交
交  于点
于点  ,连接
,连接  .
.
 中,
中,  ,把矩形沿对角线
,把矩形沿对角线  所在直线折叠,使点
所在直线折叠,使点  落在点
落在点  处,
处,  交
交  于点
于点  ,连接
,连接  .
. 
-
(1) 求证:
 ;
;
-
(2) 求证:
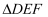 是等腰三角形.
是等腰三角形.
一件商品的原价是190元,经过两次提价后的价格为226元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
A . 190(1+x)=226
B . 190(1﹣x)=226
C . 190(1+x)2=226
D . 190(1﹣x)2=226
在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,BC=3,AC=6.
①试作出△ABC以B为旋转中心,沿顺时针方向旋转90°后的图形△BA1C1;
②若点A的坐标为(﹣3,4),试建立合适的直角坐标系,并写出B,C两点的坐标.


分解因式:![]() =_______________________.
=_______________________.
最近更新
- 台湾受灾牵动着大陆民众的心,大陆倾力为台湾同胞提供帮助。2009年8月18日下午,价值248万元的第二批援台救灾货物搭乘
- 英特尔公司副总裁肖恩·马洛克曾经说:“因特网是魔幻的第七大洲,在这里,每个人只需敲几下键盘就可以了解到世界上的所有知识。
- 图示为某探究活动小组设计的节能运动系统。斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为。木箱在轨道顶端时,自动
- 小刚同学用如图所示装置进行“粒子不断运动”的研究,一段时间后,可观察到无色酚酞溶液变红,则物质X是()A.浓氨水 B
- 当黑龙江还是冰天雪地的时候,海南岛已经开始春耕,这是由于我国( ) A.地势西高东低 B.海陆位置不同
- 下列反应中,属于氧化还原反应的是 ( )A.Fe(
- 如图a、b所示,是一辆质量m=6×103kg的公共汽车在t=0和t=4s末两个时刻的两张照片.当t=0时,汽车刚启动(
- 下列事件与其历史影响的搭配,不相符的是 ( ) A.遵义会议的召开-----中国历史上生死攸关的转折点 B.中华
- 下列离子方程式正确的是 A.用惰性电极电解饱和氯化钠溶液:2Cl- + 2H+ H2↑+ Cl2↑B.用银氨溶液检验乙醛
- ......
- 已知点A(a,2)(a>0)到直线l:x-y+3=0的距离为1,则a等于( )A. B.
- 下列属于同位素的一组是A. 水和重水 B. Na2O和Na2O2 C. 氕、氘、氚 D.
- 用酵母菌酿酒的主要阶段为:加料、接种、通气培养、密封发酵。从接种后到密封前这一阶段,酵母菌种群数量变化的曲线为
- 下列实验操作正确的是() A.
- 某温度下,Fe(OH)3(s)、Cu(OH)2(s)分别在溶液中达到沉淀溶解平衡后,改变溶液pH,金属阳离子浓度的变化如
- 2010年上海世博会实现了环保世博、生态世博的目标,下列做法中不符合这一目标的是 A.部分国家的展馆使用可降
- 电视机等家用电器的开启、关闭及频道转换,可以通过遥控器实现,遥控电视机的光是( ) A.红光 B.红
- Jenny gets upearly in the morning. She has her breakfast and
- 下图为某地地质构造简图,读图判断1~2题。1 图中岩层,最晚形成的是 () A.①
- 将镁、铝的混合物0.1 mol溶于100 mL 2 mol/L的H2S04溶液中,然后再滴加1 mol/L的NaOH溶液




