初中 数学
去括号后等于a-b+c的是( )
A . a-(b+c)
B . a-(b-c)
C . a+(b-c)
D . a+(b+c)
大众服装店今年4月用4000元购进了一款衬衣若干件,上市后很快售完,服装店于5月初又购进同样数量的该款衬衣,由于第二批衬衣进货时价格比第一批衬衣进货时价格提高了20元,结果第二批衬衣进货用了5000元.
-
(1) 第一批衬衣进货时的价格是多少?
-
(2) 第一批衬衣售价为120元/件,为保证第二批衬衣的利润率不低于第一批衬衣的利润率,那么第二批衬衣每件售价至少是多少元?
(提示:利润=售价﹣成本,利润率=
 )
)
综合与实践
如图1,已知点G在正方形ABCD的对角线AC 上,GE⊥BC,垂足为E,GF⊥CD,垂足为F.


-
(1) (证明与推断)
①四边形CEGF的形状是;
②
 的值为;
的值为; -
(2) (探究与证明)
在图1的基础上,将正方形CEGF绕点C按顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
-
(3) (拓展与运用)
如图3,在(2)的条件下,正方形CEGF 在旋转过程中,当B、E、F三点共线时,探究AG和GE的位置关系,并说明理由.
如图,在平面直角坐标系中,正方形ABCO的边长为3,点O为坐标原点,点A、C分别在x轴、y轴上,点B在第一象限内直线y=kx+1分别与x轴、y轴、线段BC交于点F、D、G,AE⊥FG,下列结论:①△GCD和△FOD的面积比为3:1:②AE的最大长度为 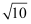 :③tan∠FEO=
:③tan∠FEO=  ④当DA平分∠EAO时,CG=
④当DA平分∠EAO时,CG=  ,其中正确的结论有( )
,其中正确的结论有( )
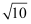 :③tan∠FEO=
:③tan∠FEO=  ④当DA平分∠EAO时,CG=
④当DA平分∠EAO时,CG=  ,其中正确的结论有( )
,其中正确的结论有( )
A . ①②③
B . ②③
C . ②③④
D . ③④
如图,数轴上表示1,  的点分别为A和B,若A为BC的中点,则点C表示的数是( )
的点分别为A和B,若A为BC的中点,则点C表示的数是( )
 的点分别为A和B,若A为BC的中点,则点C表示的数是( )
的点分别为A和B,若A为BC的中点,则点C表示的数是( ) ![]()
A .  -1
B . 1-
-1
B . 1-  C .
C .  -2
D . 2-
-2
D . 2- 
 -1
B . 1-
-1
B . 1-  C .
C .  -2
D . 2-
-2
D . 2- 
等腰三角形一腰上的高线与另一腰的夹角是50°,则这个等腰三角形的顶角为.
根据疫情防控工作需要,某社区组织甲、乙两支医疗队开展疫苗接种工作,甲队比乙队每小时多接种30人,甲队接种2250人与乙队接种1800人用时相同,问甲队每小时接种多少人?
某服装进货价80元/件,标价为200元/件,商店将此服装打x折销售后仍获利50%,则x为( )
A . 5
B . 6
C . 7
D . 8
某校为了解高一年级住校生在校期间的月生活支出情况,从高一年级600名住校学生中随机抽取部分学生,对他们今年4月份的生活支出情况进行调查统计,并绘制成如下统计图表:
| 组别 | 月生活支出x(单位:元) | 频数(人数) | 频率 |
| 第一组 | x<300 | 4 | 0.10 |
| 第二组 | 300≤x≤350 | 2 | 0.05 |
| 第三组 | 350≤x≤400 | 16 | n |
| 第四组 | 400≤x≤450 | m | 0.30 |
| 第五组 | 450≤x≤500 | 4 | 0.10 |
| 第六组 | x≥500 | 2 | 0.05 |
请根据图表中所给的信息,解答下列问题:
-
(1) 在这次调查中共随机抽取了名学生,图表中的m=,n=;
-
(2) 请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数;
-
(3) 现有一些爱心人士有意愿资助该校家庭困难的学生,学校在本次调查的基础上,经过进一步核实,确认高一(2)班有A,B,C三名学生家庭困难,其中A,B为女生,C为男生. 李阿姨申请资助他们中的两名,于是学校让李阿姨从A,B,C三名学生中依次随机抽取两名学生进行资助,请用列表法(或树状图法)求恰好抽到A,B两名女生的概率.
计算:(  +
+  )2008•(
)2008•(  ﹣
﹣  )2009=.
)2009=.
 +
+  )2008•(
)2008•(  ﹣
﹣  )2009=.
)2009=.
如果每盒水笔有10支,售价16元,用y(元)表示购买水笔的价钱,x表示购买水笔的支数,那么y与x之间的关系是.
已知p与q互为相反数,且p≠0,那么下列关系式正确的是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某车间计划在一定的时间内生产240套零配件,在生产中改进了技术,结果每天比原计划多生产4套并提前5天完成生产任务,设原计划每天生产  套零配件,则可列方程为.
套零配件,则可列方程为.
 套零配件,则可列方程为.
套零配件,则可列方程为.
抖音,是由字节跳动孵化的一款音乐创意短视频社交软件.该软件于2016年9月20日上线,是一个面向全年龄的短视频社区平台.近年来很多商家利用抖音直播平台让自己的产品大卖,某农户小王借助直播平台,计划在今年7月销售800斤奇异果,每斤奇异果定价为29元.
-
(1) 经过7月试销售,小王发现每斤奇异果售价每降低0.2元,销量将增加20斤,若计划每月奇异果的销售总量为1200斤,则每斤奇异果售价应定为多少元?
-
(2) 由于抖音直播的推广作用,奇异果的线下销售也终于迎来了复苏,在线上、线下销售单价一致的情况下,8月线上、线下的销售总额为30000元.受季节的影响,9月价格进行了一定调整,线下单价与(1)问中的售价保持一致,线上单价在(1)问的售价基础上提高了
 a%,但9月整体月销售总量仍比(1)问中的计划销售总量上涨a%,其中线下销售量占到了9月总销售量的
a%,但9月整体月销售总量仍比(1)问中的计划销售总量上涨a%,其中线下销售量占到了9月总销售量的  ,最终9月总销售额比8月增加了
,最终9月总销售额比8月增加了  a元,求a的值.
a元,求a的值.
如图,在平面直角坐标系中,点M(14,0)是x轴上的点,点P的坐标是(9,12),连接OP,PM.

-
(1) 求线段PM的长;
-
(2) 在第一象限内找一点N,使四边形OPNM是平行四边形,画出图形并求出点N的坐标(保留作图痕迹)
随着通讯技术的日新月异,中国也即将进入5G时代.某公司生产A和B两类芯片.受国际环境影响,A类芯片因技术提升销量提升,B类芯片销量有所下滑.
-
(1) 该公司3 月总销售A、B芯片共7800块,其中A类销量不超过B类销量的7倍少200块,求该公司3月销售B类芯片至少多少块?
-
(2) 该公司根据3月销售情况,调整了销售策略.该公司3月A类的销售量为2000块,销售均价为30元/块,4月A类的销量比3月增加了2m%,但销售均价比3月减少了m%;该公司3月B类的销量为1000块,销售均价为45元/块,4月B类的销量比3月减少了m%,销售均价不变,该公司4月在该区域销售的A类和B类芯片的销售总金额与其3月在该区域销售的A类和B类芯片的销售总金额相同,求m的值.
已知  是方程组
是方程组  的解,则代数式(a+b)(a-b)的值为
的解,则代数式(a+b)(a-b)的值为
 是方程组
是方程组  的解,则代数式(a+b)(a-b)的值为
的解,则代数式(a+b)(a-b)的值为
将函数y=x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|x+b|(b为常数)的图象

-
(1) 当b=0时,在同一直角坐标系中分别画出函数
 与y=|x+b|的图象,并利用这两个图象回答:x取什么值时,
与y=|x+b|的图象,并利用这两个图象回答:x取什么值时,  比|x|大?
比|x|大?
-
(2) 若函数y=|x+b|(b为常数)的图象在直线y=1下方的点的横坐标x满足0<x<3,直接写出b的取值范围
如图,AD是△ABC的中线,点E在线段AD上,且 . 若△DEC的面积是1,则△ABD的面积是( )
. 若△DEC的面积是1,则△ABD的面积是( )
 . 若△DEC的面积是1,则△ABD的面积是( )
. 若△DEC的面积是1,则△ABD的面积是( )
A . 2
B . 3
C . 4
D . 6
从甲地到乙地,公共汽车原需行驶7个小时,开通高速公路后,车速平均每小时增加了20千米,只需5个小时即可到达,求甲、乙两地的路程.
最近更新
- 研究者选取南瓜幼苗进行了无土栽培实验,如图为该幼苗的光合速率、呼吸速率随温度变化的曲线图,请分析回答相关问题.(1)A点
- 当一个活细胞中的ATP和ADP含量之比由5:2变为2:5时,这种变化过程显示细胞( ) A.储存能量 B.消
- (多选)中国首个南极内陆考察站——“中国南极昆仑站”于2009年1月27日胜利建成,如图所示,南极的最低气温大约是-89
- 已知函数f(x)在(0,2)上是增函数,且是偶函数,则、、的大小顺序是 (按从小到大的顺序)
- 已知函数f(x)=2f′(1)lnx﹣x,则f(x)的极大值为.
- If you don’t wait _______ the red light, you will be punishe
- 读我国部分地区≥l0℃积温等值线略图(单位:℃),回答14~15题 14.等值线L1、L2所示的积温数可能分别为( )
- “To meet people’s desirefor _____ happy life is our mission
- 命题“p:∃x∈R,x2+2x+a≤0”的否定形式为.
- David told me that you would like to takea trip to America,
- 14.在下面一段文字横线处补写恰当的语句,使整段文字语意完整连贯,内容贴切,逻辑严 密。每处不超过12个字。 植物最大的
- 下列物质除杂(括号内物质为杂质)的方法及试剂都正确的是物 质 方 法 试 剂 A NaCl溶液(I2) 蒸馏 CCl4
- 如图所示,A、B分别为单摆做简谐运动时摆球的不同位置.其中,位置A为摆球摆动的最高位置,虚线为过悬点的竖直线,以摆球最低
- 17世纪的荷兰或荷兰人被称作“海上马车夫”,主要是因为17世纪的荷兰或荷兰人() A.有众多商船出入世界各地,贩运商品,
- 下列实验操作,错误的是( )
- 在学习了启蒙思想之后,有同学将启蒙思想与文艺复兴作比较,得出了如下结论,你认为不正确的是 A、都是资产阶级思想
- 下列有关生物工程的叙述中,不正确的是 A.在转基因植物某个细胞中,所有基因都表达,但表达的时间不相同 B.进
- 我国已经达到的小康,还是低水平、不全面、发展很不平衡的小康。所以我们应集中力量,建设全面惠及十几亿人口更高水平的小康社会
- 2008年我国节假日进行了调整,端午节已被定为国家法定节日,这一天人们有划龙舟、吃粽子的习俗,这是为了纪念 A.屈原
- 乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥和引桥两部分组成(如图所示).建造前工程师用以下方式做了测量;无人机在处正



