初中 数学
如图,在平面直角坐标系中,四边形 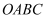 是菱形,若点
是菱形,若点  的坐标是
的坐标是  ,则点
,则点  的坐标是.
的坐标是.
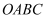 是菱形,若点
是菱形,若点  的坐标是
的坐标是  ,则点
,则点  的坐标是.
的坐标是. 
某社区超市第一次用2000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的2倍少4件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
|
甲 |
乙 |
|
|
进价(元/件) |
20 |
25 |
|
售价(元/件) |
27 |
35 |
-
(1) 该超市购进甲、乙两种商品各多少件?
-
(2) 该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
-
(3) 该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的2倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润是546元,求第二次乙商品是按原价打几折销售?
下列方程变形正确的是( )
A . 由3﹣x=﹣2得x=3+2
B . 由3x=﹣5得x=﹣ C . 由
C . 由 y=0得y=4
D . 由4+x=6得x=6+4
y=0得y=4
D . 由4+x=6得x=6+4
 C . 由
C . 由 y=0得y=4
D . 由4+x=6得x=6+4
y=0得y=4
D . 由4+x=6得x=6+4
计算:
-
(1)

-
(2)

已知关于x的不等式组

-
(1) 当
 时,求该不等式组的整数解;
时,求该不等式组的整数解;
-
(2) 若原不等式组的整数解只有7,8,求m的取值范围.
如图,O是四边形ABCD内一点,E是CD边的中点,分别连接OA,OB,OC,OD,OE,已知OA=OD,OB=OC,∠AOB+∠COD=180°.求证:OE=  AB.
AB.
 AB.
AB. 
过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形是边形.
等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角的度数为.
用适当的方法解下列方程:
-
(1) 2x2﹣8x=0.
-
(2) x2﹣3x﹣4=0.
求出抛物线的开口方向、对称轴、顶点坐标.
-
(3) y=
 x2﹣x+3(公式法).
x2﹣x+3(公式法).
如图所示,矩形 中,
中, ,
,  , 点M在边
, 点M在边 上,若
上,若 平分
平分 , 则
, 则 的长是.
的长是.
 中,
中, ,
,  , 点M在边
, 点M在边 上,若
上,若 平分
平分 , 则
, 则 的长是.
的长是.
概念学习
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形  不是等腰三角形
不是等腰三角形  一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
-
(1) 理解概念:如图1,在
 中,
中,  ,
,  ,请写出图中两对“等角三角形”
,请写出图中两对“等角三角形” 
-
(2) 概念应用:如图2,在
 中,CD为角平分线,
中,CD为角平分线,  ,
,  .求证:CD为
.求证:CD为  的等角分割线.
的等角分割线. 
如图,直线y=kx+2与x轴交于点A(3,0),与y轴交于点B , 抛物线y=﹣  x2+bx+c经过点A , B .
x2+bx+c经过点A , B .
 x2+bx+c经过点A , B .
x2+bx+c经过点A , B . 
-
(1) 求k的值和抛物线的解析式;
-
(2) M(m , 0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P , N .
①若以O , B , N , P为顶点的四边形是平行四边形时,求m的值.
②连接BN , 当∠PBN=45°时,求m的值.
如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.

-
(1) 求证:ED∥AB;
-
(2) OF平分∠COD交DE于点F,若∠OFD=65°,求∠1的度数.
如图,已知在数轴上有三个点A,B,C,O是原点,其中A,B,C三点表示的数分别是40,80,120,动点P从点O出发向右以每秒4个单位的速度匀速运动;同时,动点Q从点C出发,在数轴上向左匀速运动,速度为v(v>1);运动时间为t.

-
(1) 求:点P从点O运动到点C时,运动时间t的值.
-
(2) 若Q的速度v为每秒6个单位,那么经过多长时间P,Q两点相距60个单位?此时|QB﹣QC|是多少?
-
(3) 当|PA+PB|=2|QB﹣QC|=48时,请求出点Q的速度v的值.
![]() ÷
÷![]()
若实数a、b满足|a+2|+![]() =0,求
=0,求![]() 的值.
的值.
计算
(-1)×a.
已知a2﹣a﹣3=0,那么代数式![]()
![]() 的值是 .
的值是 .
已知正比例函数![]() 的函数值随的增大而增大,则一次函数
的函数值随的增大而增大,则一次函数![]() 的图象大致是( )
的图象大致是( )

在Rt△ABC中,∠ACB=90°,∠CAB=36°,在直线AC或BC上取点M,使得△MAB为等腰三角形,符合条件的M点有___________个
最近更新
- 中共十七届五中全会指出,要推动文化大发展大繁荣、推动文化产业成为国民经济支柱性产业,充分发挥文化引导社会、教育人民、推动
- 研究表明,迄今为止世界上还没有一个国家能够对每次大地震作出准确预报。据介绍,我国虽有一定的监测能力,但对于地壳深部的探测
- 雾是近地面大气层中大量微小水滴或冰晶组成的悬浮体。2006年入冬以来,济南遭遇多次大雾天气,大部分地区能见度小于1公里,
- 在探索遗传本质的过程中,科学发现与使用的研究方法配对正确的是 ①1866年孟德尔的豌豆杂交实验,提出遗传规律 ②1903
- 在光滑的水平面内建立如图所示的直角坐标系,长为L的光滑细杆AB的两个端点分别被约束在x轴和y轴上,现让杆的A端沿x轴正方
- 下列离子方程式正确的是
- 生活中常见的下列现象,只发生物理变化的是 A.高粱酿酒 B.保
- 1. 若用“R”表示显性基因,“r”表示隐性基因,则图1中子代高茎豌豆的基因型为A. RR
- 宋应星在《天工开物》序言中写道:“丐大业文人,弃掷案头!此书于功名进取毫不相关也!”由此可见 A.宋应星对明代科举束缚人
- (1)完成下列反应的文字表达式,并注明反应的基本类型. ①铁丝在氧气中燃烧; ②高锰酸钾制氧气; (2)在下列物质中:①
- ____ to get a ticket for the 2006 FIFA World Cup, George has
- 2014年2月24日,国家统计局公布统计数据,城镇居民人均可支配收入实际增长7.0%,农村居民人均纯收入实际增长9.3%
- 下列物质性质与应用对应关系正确的是() A.氨气具有还原性,可用于检查HCl泄漏 B.浓硫酸具有脱水性,可用于干燥CO2
- 丁烷的一氯代物共有多少种 ( ) A.3 B.5 C.4
- 下列命名正确的是 A、 2—乙基丁烷 B、 3,4-二甲基戊烷C、 4
- 下列现象中与善良格格不入的心态和行为是 ( )①对别人的优点.成就心怀妒忌,中伤、贬低②对别人的缺点吹毛求疵,讽刺
- 如下图是一组有规律的图案,第1个 图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n(n是正整数)个图案中
- 17.阅读下面这幅漫画,回答问题。(5分) (1)简要说明漫画的主要内容。(2分) (2)这幅漫画想要表达怎样的期望?(
- Tom ______to paint the fence but he got his friends to do it
- 爱迪生一生有一千多项发明,他一天工作18个小时,他却说一生从来未做过一天工作,这是因为( ) A.他喜欢工作 B



