初中数学：七年级　 八年级　 九年级　 中考　

初中数学

关于 x 的方程 a（x+m）²+b=0 的解是 x₁=﹣2，x₂=1（a，m，b 均为常数，a≠0），则方程 a（x+m+2）²+b=0 的解是（）

A . x₁=0，x₂=3 B . x₁=﹣4，x₂=﹣1 C . x₁=﹣4，x₂=2 D . x₁=4，x₂=1

某人打靶五次的环数如下：1，4，6，8，x，其中整数x是这组数据的中位数，那么这组数据的平均数是（）

A . 4.8 B . 4.8或5 C . 4.6或4.8 D . 4.6或4.8或5

下列平面图形中，不是轴对称图形的是（）

A .

B .

C .

D .

小文买了一支温度计，回家后发现里面有一个小气泡（即不准确了），先拿它在冰箱里试一下，在标准温度是零下7℃时，显示为 $\text{[math]}$ ℃，在36℃的温水中，显示为32℃，那么用这个温度计量得的室外气温是23℃，则室外的实际气温应是（）

A . 27℃ B . 19℃ C . 23℃ D . 不能确定

薄薄的硬币在桌面上转动时看上去象球，这说明了点线面体的关系.

福布斯中文网微博通报数据显示，天猫双11成交额已经在活动开始后的60分钟内突破122亿元人民币．则122亿用科学记数法来表示是（）

A . 1.22×10¹⁰ B . 122×10⁸ C . 12.2×10⁹ D . 1.22×10⁹

已知a+2=b-1，以下等式错误的是（）

A . 2a+2=a+b-1 B . a-3=b-6 C . -a+2=-b+1 D . $\text{[math]}$ = $\text{[math]}$

如图，在菱形ABCD中，点E是边AD上一点，延长AB至点F，使BF=AE，连接BE、CF求证：BE=CF。

如图，为了测得电视塔的高度AB，在D处用高为1米的测角仪CD，测得电视塔顶端A的仰角为30°，再向电视塔方向前进100米达到F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB（单位：米）为（　　）

A . $\text{[math]}$ B . 51 C . $\text{[math]}$ D . 101

已知：如图，在平面直角坐标系中，有菱形OABC，点A的坐标为（10，0），对角线OB、AC相交于点D，双曲线y= $\text{[math]}$ （x＞0）经过点D，交BC的延长线于点E，且OB•AC=160，有下列四个结论：

①双曲线的解析式为y= $\text{[math]}$ （x＞0）；

②点C的坐标是（6，8）；

③sin∠COA= $\text{[math]}$ ；

④AC+OB=6 $\text{[math]}$ ．

其中正确的结论有（　　）

A . 1个 B . 2个 C . 3个 D . 4个

如图，现要在抛物线 $\text{[math]}$ 上找点 $\text{[math]}$ ，针对b的不同取值，所找点P的个数，四人的说法如下：

甲：若 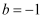$\text{[math]}$ ，则点P的个数为3；

乙：若 $\text{[math]}$ ，则点P的个数为1；

丙：若 $\text{[math]}$ ，则点P的个数为1；

丁：若 $\text{[math]}$ ，则点P的个数为0.

其中说法正确的有（）

A . 0个 B . 1个 C . 2个 D . 3个

下列说法正确的是（）

①若 $\text{[math]}$ 是关于x的方程 $\text{[math]}$ 的一个解，则 $\text{[math]}$ ；②在等式 $\text{[math]}$ 两边都除以3，可得 $\text{[math]}$ ；③若 $\text{[math]}$ ，则关于x的方程 $\text{[math]}$ 的解为 $\text{[math]}$ ；④在等式 $\text{[math]}$ 两边都除以 $\text{[math]}$ ，可得 $\text{[math]}$ ．