初中 数学
如图1,已知抛物线  的对称轴是直线
的对称轴是直线 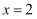 ,且经过点
,且经过点  ,抛物线与x轴相交于A,B两点(B点在A点右侧).
,抛物线与x轴相交于A,B两点(B点在A点右侧).
 的对称轴是直线
的对称轴是直线 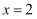 ,且经过点
,且经过点  ,抛物线与x轴相交于A,B两点(B点在A点右侧).
,抛物线与x轴相交于A,B两点(B点在A点右侧). 
-
(1) 求抛物线的解析式和A,B两点的坐标;
-
(2) 如图2,已知
 ,
,  ,
,  ,点P是第一象限的抛物线
,点P是第一象限的抛物线  上的一点.
上的一点. ①当
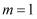 时,求使四边形EFPQ的面积最大时的点P的坐标;
时,求使四边形EFPQ的面积最大时的点P的坐标;②若
 ,求m为何值时,四边形EFPQ的周长最小?
,求m为何值时,四边形EFPQ的周长最小?
当x为何值时,式子  ﹣3比式子﹣
﹣3比式子﹣ 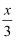 +1的值小1?
+1的值小1?
 ﹣3比式子﹣
﹣3比式子﹣ 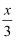 +1的值小1?
+1的值小1?
下列几组数中是勾股数的是( )
A .  、
、  、1
B . 3,4,6
C . 5,12,13
D . 0.9,1.2,1.5
、1
B . 3,4,6
C . 5,12,13
D . 0.9,1.2,1.5
 、
、  、1
B . 3,4,6
C . 5,12,13
D . 0.9,1.2,1.5
、1
B . 3,4,6
C . 5,12,13
D . 0.9,1.2,1.5
完成下面的证明(在括号中填写推理理由)如图,已知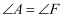 ,
, 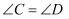 , 求证:
, 求证: .
.
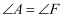 ,
, 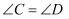 , 求证:
, 求证: .
. 
证明:因为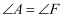 ,
,
所以 ( ▲ ),
( ▲ ),
所以 ▲
▲  ( ▲ ).
( ▲ ).
因为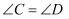 ,
,
所以 ▲
▲  ( ▲ ),
( ▲ ),
所以 ( ▲ ).
( ▲ ).
下列命题错误的是( )
A . 相似三角形周长之比等于对应高之比
B . 两个等腰直角三角形一定相似
C . 各有一个角等于91°的两个等腰三角形相似
D . 两边对应成比例且有一个角相等的两个三角形相似
某水果商场经销一种高档水果,原价每千克50元.
-
(1) 连续两次降价后每千克32元,若每次下降的百分率相同.求每次下降的百分率;
-
(2) 若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,但商场规定每千克涨价不能超过8元,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,那么每千克应涨价多少元?
如图,四边形ABCD是矩形, 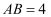 ,
,  ,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是.
,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是.
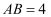 ,
,  ,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是.
,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是. 
已知一次函数y=3x+p和y=x+q的图象都经过点A(﹣2,0),且与y轴分别交于B、C两点,求△ABC的面积.
如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是。

某网店安踏牌运动鞋以a元的价格卖出,利润率为20%,则该运动鞋的成本为( )
A .  元
B .
元
B .  元
C .
元
C .  元
D .
元
D .  元
元
 元
B .
元
B .  元
C .
元
C .  元
D .
元
D .  元
元
在函数y= 中,自变量x的取值范围是
中,自变量x的取值范围是
 中,自变量x的取值范围是
中,自变量x的取值范围是
如图所示,在△ABC中,点D是BC上的一点,已知AC=CD=5,AD=6,BD=  ,则△ABC的面积是( )
,则△ABC的面积是( )
 ,则△ABC的面积是( )
,则△ABC的面积是( ) 
A . 18
B . 36
C . 72
D . 125
下列命题中,错误的是( )
A . 一组对边平行,另一组对边相等的四边形是平行四边形
B . 矩形既是轴对称图形,又是中心对称图形
C . 菱形的一条对角线平分一组对角
D . 对角线相等且互相垂直平分的四边形是正方形
解方程:  .
.
 .
.
已知∠A=47°,则∠A的余角等于度.
先填写表,通过观察后再回答问题:
|
a |
0 |
0.0001 |
0.01 |
1 |
100 |
10000 |
… |
|
| 0 | 0.01 | x | 1 | y | 100 | … |
-
(1) 表格中x=,y=;
-
(2) 从表格中探究a与
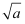 数位变化可以发现:当被开方数a每扩大100倍时,
数位变化可以发现:当被开方数a每扩大100倍时, 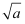 扩大倍,请你利用这个规律解决下面两个问题:
扩大倍,请你利用这个规律解决下面两个问题: ①已知
 ,则
,则  ;
;②已
 ,若
,若  ,用含m的代数式表示n , 则n=;
,用含m的代数式表示n , 则n=; -
(3) 请根据表格提示,试比较
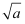 与a的大小.
与a的大小.
出租车司机老黄每天下午都在东西走向的大道上载客营运,若规定向东为正,向西为负,这天下午行走里程(单位:千米)如下:﹣160,+100,﹣20,+50,﹣20,﹣10.
-
(1) 将最后一名乘客送到目的地时,老黄离下午出车时的出发点多远?此时在出车时间的东边还是西边?
-
(2) 若汽车每千米耗油0.25升,每升汽油5.5元,求:这天下午老黄开的车共耗油多少升?共花多少元油费?
如图1,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃.那么最省事的办法是带( )去配.
(A) ① (B) ②
(C) ③ (D) ①和②

小名的父亲饭后出去散步,从家走20分钟到一个离家900米的报亭,看10分钟报纸后,用15分钟返回家里.下面四个图象中,表示小明父亲的离家距离与时间之间关系的是( )




A. A B. C. D.
在矩形ABCD中,AB=5,AD=12,P是AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF=__________.

最近更新
- 有关世界海陆分布的叙述,正确的是
- ---Can you paint? ---________. A.Yes, a lit
- Are you worried by the rising crime rate? If you are, then y
- 李奶奶家住某老旧小区的六层,上下楼很不方便。大家一直盼着小区加装电梯,但一、二层住户因为担心影响采光和噪音干扰,坚决反对
- 地球赤道上的物体重力加速度为g,物体在赤道上随地球自转的向心加速度为a,要使赤道上的物体“飘”起来,则地球的转速应为原来
- 矩形线框绕垂直于匀强磁场且在线框平面的轴匀速转动时产生了交变电流,下列说法正确的是( )A.当线框位于中性面时,线
- 下列有关细胞的叙述,正确的是() A. 病毒是一类具有细胞结构的生物 B. 蓝藻细胞具有细胞
- 以下是对现代生物进化理论的一些理解,其中错误的是 A.环境改变使生物产生适应性的变异
- 电阻R1、R2交流电源按照图甲所示方式连接,R1=10 Ω,R2=20 Ω。合上开关后S后,通过电阻R2的正弦交变电流i
- 《三国演义》写尽了十八般兵器,但没有写到枪炮;《封神榜》写尽商纣宫廷的奢华,却没有提到互联网、高尔夫。这是因为 A.意识
- 2006年是中国工农红军长征胜利70周年。 读图1和表,回答问题: 图1 表:地区 资源潜在总值 占全国比重(%)
- 若y=∫(sin t+cos tsin t)dt,则y的最大值是()A.1 B.2 C.-
- 下面这篇报道有不少语病,请找出其中三处进行修改。 星期三,校团总支召开座谈会。①到会的15名与会者,②就共青团员如何为社
- 直线l经过点P(﹣3,4)且与圆x2+y2=25相切,则直线l的方程是() A.y﹣4=﹣(x+3) B.y﹣4=
- 图示法是学习历史的一种好方法.它能将复杂的历史较直观形象的展示出来。下面哪幅图直观反映了三国鼎立的形势 ( )
- 科学家屠呦呦因创制新型抗疟药﹣﹣青蒿素和双氢青蒿素的贡献,获得2015年诺贝尔医学奖,下列关于青蒿素(化学式C15H22
- 下列运算正确的是( ) A.+ = B.×= C. =3-1 D. =5-3
- 在利用光具座进行凸透镜成像的实验探究中: (1)如下图所示,一束平行于凸透镜主光轴的光线经过凸透镜后,在光屏上形成
- 某溶液中含有HCO3―、SO32―、Na+、CH3COO―等4种阴离子。若向其中加入足量的Na2O2后,溶液中离子浓度基
- 在图中的〇里填上适当的电表符号,使之成为正确的电路图。



