初中 数学
化简(  +a﹣2)÷
+a﹣2)÷  .
.
 +a﹣2)÷
+a﹣2)÷  .
.
已知实数a在数轴上的对应点,如图所示,则化简 所得结果为
所得结果为 
如图,直线AB、CD相交于点E,DF∥AB,若∠D=50°,则∠AEC的度数等于( )

A . 130°
B . 120°
C . 150°
D . 50°
设  =x,由
=x,由  =0.777…可知,10x=7.777…,所以10x-x=7.解方程x=
=0.777…可知,10x=7.777…,所以10x-x=7.解方程x= 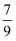 .于是,得
.于是,得  =
= 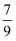 .则无限循环小数
.则无限循环小数  化成分数等于.
化成分数等于.
 =x,由
=x,由  =0.777…可知,10x=7.777…,所以10x-x=7.解方程x=
=0.777…可知,10x=7.777…,所以10x-x=7.解方程x= 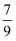 .于是,得
.于是,得  =
= 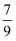 .则无限循环小数
.则无限循环小数  化成分数等于.
化成分数等于.
如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是 °.

下列因式分解正确的是( )
A . x2+9=(x+3)2
B . a2+2a+4=(a+2)2
C . a3-4a2=a2(a-4)
D . 1-4x2=(1+4x)(1-4x)
下列四个点,在正比例函数y=−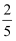 x的图象上的点是( )
x的图象上的点是( )
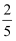 x的图象上的点是( )
x的图象上的点是( )
A . (2,5)
B . (5,2)
C . (2,-5)
D . (5,-2)
某水泥仓库6天内进出水泥的吨数如下(“+”表示进库,“-”表示出库):
+20、-25、-13、+28、-29、-16.
-
(1) 经过这6天,仓库里的水泥是增多还是减少了?增多或减少了多少吨?
-
(2) 经过这6天,仓库管理员结算发现库里还存200吨水泥,那么6天前,仓库里存有水泥多少吨?
-
(3) 如果进出仓库的水泥装卸费都是每吨5元,那么这6天要付多少元装卸费?
数学课上,李老师出示了明代数学家程大位的《算法统宗》中的一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两(注:明代时1斤=16两,故有“半斤八两”这个成语).给出四种设未知数及列方程(组)的思路:①设有x人分银子,据题意得  ;②设所分银子有y两,据题意得
;②设所分银子有y两,据题意得  ;③设所分银子有t两,据题意得
;③设所分银子有t两,据题意得  ;④设有m人分银子,所分银子有n两,根据题意得
;④设有m人分银子,所分银子有n两,根据题意得  ,其中正确的是( )
,其中正确的是( )
 ;②设所分银子有y两,据题意得
;②设所分银子有y两,据题意得  ;③设所分银子有t两,据题意得
;③设所分银子有t两,据题意得  ;④设有m人分银子,所分银子有n两,根据题意得
;④设有m人分银子,所分银子有n两,根据题意得  ,其中正确的是( )
,其中正确的是( ) | 隔墙听得客分银, 不知人数不知银. 七两分之多四两, 九两分之少半斤. (算法统宗) |
A . ①和②
B . ①和③
C . ②和④
D . ③和④
一个数的算术平方根与这个数的立方根的和为0,则这个数是( )
A . ﹣1
B . ±1
C . 0
D . 不存在
用简便方法计算:
-
(1) 982;
-
(2) 99×101.
如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )

A . 70°
B . 110°
C . 130°
D . 140°
为了实施乡村振兴战略,帮助农民增加收入,市政府大力扶持农户发展种植业,每亩土地每年发放种植补贴120元.张远村老张计划明年承租部分土地种植某种经济作物.考虑各种因素,预计明年每亩土地种植该作物的成本y(元)与种植面积x(亩)之间满足一次函数关系,且当  时,
时,  ;当
;当  时,
时,  .
.
 时,
时,  ;当
;当  时,
时,  .
.
-
(1) 求y与x之间的函数关系式(不求自变量的取值范围);
-
(2) 受区域位置的限制,老张承租土地的面积不得超过240亩.若老张明年销售该作物每亩的销售额能达到2160元,当种植面积为多少时,老张明年种植该作物的总利润最大?最大利润是多少?(每亩种植利润=每亩销售额-每亩种植成本+每亩种植补贴)
把一些书分给几名同学,如果每人分  本,那么余
本,那么余  本;如果前面的每名同学分
本;如果前面的每名同学分  本,那么最后一人就分不到
本,那么最后一人就分不到  本,这些书有______本,共有______人.( )
本,这些书有______本,共有______人.( )
 本,那么余
本,那么余  本;如果前面的每名同学分
本;如果前面的每名同学分  本,那么最后一人就分不到
本,那么最后一人就分不到  本,这些书有______本,共有______人.( )
本,这些书有______本,共有______人.( )
A .  本,
本, 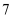 人
B .
人
B .  本,
本,  人
C .
人
C .  本,
本,  人
D .
人
D .  本,
本,  人
人
 本,
本, 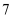 人
B .
人
B .  本,
本,  人
C .
人
C .  本,
本,  人
D .
人
D .  本,
本,  人
人
如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E。

-
(1) 求证:DE=AB;
-
(2) 以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,试求
 的长。
的长。
用式子表示“比x的倒数小5的数”是.
如图,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11…的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4…则第一个黑色梯形的面积S1= 4 ;观察图中的规律,第n(n为正整数)个黑色梯形的面积Sn= .

请用因式分解法解方程: ![]()
当10kg的菜放在称上时,指示盘上的指针转了180°,当1.5kg的菜放在称上时,指针转过__________度,如果指针转了36°,这些菜有___________kg.
下面是某同学在一次测试中的计算:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中运算正确的个数为( )
,其中运算正确的个数为( )
A.4个 B.3个 C.2个 D.1个
最近更新
- 如图所示,等臂天平处于平衡状态。则左盘物块的密度是:A.1.4克/厘米; B.2.0克/厘米; C.3.
- 已知:①C(s)+O2(g)CO2(g) ΔH=-393.5kJ·mol-1 ②2H2(g)+O2(g)2H2O(l
- 据报道,纳米Fe3 O4 晶体材料可以作为核磁共振造影增强剂,用于疾病的诊断和作为药物载体用于疾病的治疗。其制备过程如图
- 如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C. (1)求k的值; (2)
- The first time I saw her, Mary was standing still in the win
- 已知的三边长为所在平面内一点,若,则点是的( ) 外心 内心 重心
- 若4a2﹣2ka+9是一个完全平方式,则k=() A.12 B.±12 C.6 D.±6
- 如图所示,直线A为电源的路端电压与总电流关系的伏安图线,直线B为电阻R两端电压与通过该电阻电流关系的伏安图线,用该电源和
- 关于单摆,下列认识中正确的是( ) A.一根线系着一个球悬挂起来,这样的装置就是单摆 B.可以看成单摆的装置中,细
- 下列各句中,没有语病的一句是( )(3分) A.教育部统汁数据显示,邵逸夫先生自1985年以来,连年向内地教育捐赠巨
- 已知抛物线的焦点与椭圆的一个焦点重合,它们在第一象限内的交点为,且与轴垂直,则椭圆的离心率为( ) A.B. C.
- 某化学兴趣小组为了测定一工厂废水中硫酸的质量分数,取100g废水于烧杯中,加入80g质量分数为10%的氢氧化钠溶液,恰好
- 20世纪,希尔做了以下实验:把绿叶研磨过滤,得到含有叶绿体的滤液,放在阳光下,可见滤液中有气泡产生,若放在黑暗处,则滤液
- 用燃烧法除去密闭容器中空气成分里的氧气,应选择下列物质中的()A. 细铁丝 B. 红磷 C. 硫粉 D. 木炭
- 已知函数的最小正周期为π,将y=f(x)的图象向左平移|φ|个单位长度,所得图象关于y轴对称,则φ的一个值是( )
- 当 时,二次函数 有最小值______________.
- 13.补写出下列名篇名句中的空缺部分。(6分) (1)浊酒一杯家万里, 。
- 第二节 完形填空(共20小题,每小题1.5分,满分30分) 阅读下面短文,掌握大意,然后从36-55各小题所给四个选项(
- 电流互感器和电压互感器如图所示。其中n1、n2 、n3、n4分别为四组线圈的匝数,a、b为两只交流电表,则 A.A为电流
- 14.(2012·北京市西城区期末)下图表示基因控制胰岛素合成过程的示意图,请分析并回答:(1)DNA分子基本骨架由__



