初中 数学
图1是某长征主题公园的雕塑,将其抽象成如图2所示的示意图,已知 , A,D,H,G四点在同一直线上,测得
, A,D,H,G四点在同一直线上,测得 . (结果保留小数点后一位)
. (结果保留小数点后一位)
 , A,D,H,G四点在同一直线上,测得
, A,D,H,G四点在同一直线上,测得 . (结果保留小数点后一位)
. (结果保留小数点后一位)
-
(1) 求证:四边形
 为平行四边形;
为平行四边形;
-
(2) 求雕塑的高(即点G到
 的距离).
的距离).(参考数据:
 )
)
在下列各式中正确的是( )
A .  =-2
B .
=-2
B . 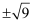 =3
C .
=3
C . 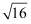 =8
D .
=8
D .  =2
=2
 =-2
B .
=-2
B . 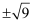 =3
C .
=3
C . 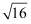 =8
D .
=8
D .  =2
=2
如图,▱ABCD中,对角线AC与BD相交于O,EF是过点O的任一直线交AD于点E,交BC于点F,猜想OE和OF的数量关系,并说明理由.

如图在平面直角坐标系内,以点C(1,1)为圆心,2为半径作圆,交x轴于A、B两点,开口向下的抛物线经过A、B两点,且其顶点P在⊙C上。
(1)写出A、B两点的坐标;
(2)确定此抛物线的解析式;
解方程:
-
(1) 4x-3(20-x)=6x-7(9-x).
-
(2)
 .
.
已知:如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点,若CE=8,则DF的长是.

数学老师在课堂上提出一个问题:“通过探究知道:  ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用  ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
 ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用  ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:-
(1)
 的小数部分是a,
的小数部分是a, 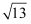 的整数部分是b,求a+b﹣
的整数部分是b,求a+b﹣  的值.
的值.
-
(2) 已知8+
 =x+y,其中x是一个整数,0<y<1,求3x+(y﹣
=x+y,其中x是一个整数,0<y<1,求3x+(y﹣  )2018的值.
)2018的值.
如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )

A . 240°
B . 360°
C . 480°
D . 540°
如图是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形,这样的白色小正方形有个.

如图,D为直角△ABC的斜边AB上一点,DE⊥AB交AC于E,如果△AED沿DE翻折,A恰好与B重合,联结CD交BE于F,如果AC═8,tanA═  ,那么CF:DF═
,那么CF:DF═
 ,那么CF:DF═
,那么CF:DF═ 
如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )

A . AD=BC,AD∥BC
B . AD∥BC,AB=DC
C . AD=BC,AB=DC
D . AD∥BC,AB∥DC
把直线y=﹣x﹣3向上平移m个单位,与直线y=2x+4的交点在第二象限,则m的取值范围是.
如图,点 在平行四边形
在平行四边形 的边
的边 上,
上, . 若
. 若 ,
,  , 则
, 则 的度数为.
的度数为.
 在平行四边形
在平行四边形 的边
的边 上,
上, . 若
. 若 ,
,  , 则
, 则 的度数为.
的度数为.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,![]() 于点E,DA平分
于点E,DA平分![]() .
.
(1)试说明AE是⊙O的切线;
(2)如果AB= 4,AE=2,求⊙O的半径.
 |
烟花厂为长沙橘子洲头周六晚上的烟花表演特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=-![]() t2+20t+1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
t2+20t+1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
A.3 s B.4 s C.5 s D.6 s
计算(![]()
![]() +
+![]()
![]() )(
)(![]()
![]() ﹣
﹣![]()
![]() )的结果为
)的结果为
如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F,
求证:∠BAE=∠DCF。

在![]() ABCD中,AD=3cm,AB=2cm,则
ABCD中,AD=3cm,AB=2cm,则![]() ABCD的周长等于( )
ABCD的周长等于( )
A.10cm B.6cm C.5cm D.4cm
下列计算正确的是( )
A.(x+2)(x﹣2)=x2﹣2 B.(a+b)(b﹣a)=a2﹣b2
C.(﹣a+b)2=a2﹣2ab+b2 D.(﹣a﹣b)2=a2﹣2ab+b2
最近更新
- 影响文化发展的因素很多,其中决定着社会制度变化和文化发展方向的是( ) A.生产力与生产关系的矛盾运动 B.科
- 自2015年6月19日端午节最后一个交易日至7月中旬,股市连续大跌,几度出现千股跌停的局面,股市情绪转向悲观。为增强市场
- (08年岳阳一中质检)如图所示,一个小物体沿光滑斜面由A点上方静止开始加速下滑,在它通过的路程中取AE并分成相等的4段,
- 双曲线虚轴的一个端点为M,两个焦点F1、F2,∠F1MF2=120°,则双曲线的离心率为( ) A.
- 20世纪90年代,我国科学家通过转基因技术将细菌的抗虫基因成功地转移到棉花的受精卵中,培育出抗虫效果明显的棉花新品种。以
- 按下列过程,最终目的能实现的是( ) A.Fe FeCl2溶液FeCl3溶液FeCl3晶体B.CuCuOCuSO4
- 烷烃A(C6H14)结构中共有四个甲基,能生成三种一氯代产物B、C、D。 B和D分别与强碱的醇溶液共热,都只能得到有机化
- (一)阅读下面两首宋诗,完成6~7题。 送别杜审言① 宋之问 卧病人事绝, 嗟君万里行。河桥不相送, 江树远含情。 别路
- The plane must be ready within half an hour. There should be
- 某实验小组使用下列器材来测定小灯泡的功率:待测小灯泡(额定电流0.5A,额定功率不大于1.5W)、电压表(3V、15V双
- 如图所示的电路,合上开关,小灯泡正常发光若将小灯泡和电流表的位置互换,则合上开关后的现象是A.小灯泡不发光
- 下列各项,体现文艺复兴与宗教改革共同点的是 ( ) A.反对禁欲
- 已知函数f(x)=|x-1|+|x-a|.若不等式f(x)≥a恒成立,求实数a的取值范围.
- 下列句子成语使用正确的一项是( ) A.阳春三月,桃红柳绿,蜂飞蝶舞,春意阑珊,徜徉于美丽的田野村落,无处不充溢着大
- 目前,我国部分地区出现了“土地换股权”模式,该模式的实质在于,在农村土地流转和村办企业建设过程中,农民可以将土地承包权作
- The red suitcase is expensive _________it’s made of leather.
- 下图是生态系统能量流动的图解。有关叙述错误的是A.方框的大小可表示该营养级生物个体数量的多少 B.通常情况下,C所获得的
- 秦灭六国后,秦王赢政兼采古史及传说中的“三皇”、“五帝”之名而称“皇帝”,其首要目的是 A.宣扬托古改制 B.承袭华
- 完形填空。 In recent(最近) years, computer games have become morean
- 已知且若,则[x]+[y]等于(其中[x]表示不超过x的最大整数 ( )



