初中 数学
已知,如图一次函数y1=ax+b与反比例函数y2=  的图象如图示,当y1<y2时,x的取值范围是( )
的图象如图示,当y1<y2时,x的取值范围是( )
 的图象如图示,当y1<y2时,x的取值范围是( )
的图象如图示,当y1<y2时,x的取值范围是( ) 
A . x<2
B . x>5
C . 2<x<5
D . 0<x<2或x>5
如图所示,将形状、大小完全相同的“  ”和线段按照一定规律摆成下列图形,第1幅图形中“
”和线段按照一定规律摆成下列图形,第1幅图形中“  ”的个数为
”的个数为  ,第2幅图形中“
,第2幅图形中“  ”的个数为
”的个数为  ,第3幅图形中“
,第3幅图形中“  ”的个数为
”的个数为  ,…,以此类推,则
,…,以此类推,则  的值为()
的值为()
 ”和线段按照一定规律摆成下列图形,第1幅图形中“
”和线段按照一定规律摆成下列图形,第1幅图形中“  ”的个数为
”的个数为  ,第2幅图形中“
,第2幅图形中“  ”的个数为
”的个数为  ,第3幅图形中“
,第3幅图形中“  ”的个数为
”的个数为  ,…,以此类推,则
,…,以此类推,则  的值为()
的值为() 
A . 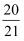 B .
B .  C .
C .  D .
D . 
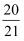 B .
B .  C .
C .  D .
D . 
如果反比例函数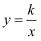 的图像经过点(-3,-4),那么函数的图象应在( )
的图像经过点(-3,-4),那么函数的图象应在( )
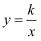 的图像经过点(-3,-4),那么函数的图象应在( )
的图像经过点(-3,-4),那么函数的图象应在( )
A . 第一、三象限
B . 第一、二象限
C . 第二、四象限
D . 第三、四象限
已知关于x的方程mx+3=4的解为x=1,则直线y=(m-2)x-3一定不经过第象限.
一个不等式的解集如图所示,则这个不等式的正整数解是.

一辆汽车以50 km/h的速度行驶,行驶的路程s km与行驶的时间t h之间的关系式为s=50 t,其中变量是( )
A . 速度与路程
B . 速度与时间
C . 路程与时间
D . 三者均为变量
化简:
-
(1)

-
(2)

如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC和一点O,△ABC的顶点和点O均与小正方形的顶点重合.

①在方格纸中,将△ABC向下平移5个单位长度得到△A1B1C1,请画出△A1B1C1;
②在方格纸中,将△ABC绕点O旋转180°得到△A2B2C2,请画出△A2B2C2.
小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )

A . ①,②
B . ②,③
C . ③,④
D . ①,④
教师运动会中,甲,乙两组教师参加“两人背夹球”往返跑比赛,即:每组两名教师用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.若距起点的距离用y(米)表示,时间用x(秒)表示.下图表示两组教师比赛过程中y与x的函数关系的图象.根据图象,有以下四个推断:
①乙组教师获胜②乙组教师往返用时相差2秒③甲组教师去时速度为0.5米/秒④返回时甲组教师与乙组教师的速度比是2:3
其中合理的是( )

A . ①②
B . ①③
C . ②④
D . ①④
如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时20海里的速度向东航行到B处,测得小岛C在北偏东30°方向上,船以原来的速度继续向东航行2小时,到达岛C正南方点D处,船从A到D一共航行了多少海里?

物理实验证实:在弹性限度内,某弹簧长度y(  )与所挂物体质量x(
)与所挂物体质量x( 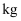 )满足函数关系
)满足函数关系  .下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
.下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
 )与所挂物体质量x(
)与所挂物体质量x( 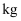 )满足函数关系
)满足函数关系  .下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
.下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系. | x | 0 | 2 | 5 |
| y | 15 | 19 | 25 |
-
(1) 求y与x的函数关系式;
-
(2) 当弹簧长度为20
 时,求所挂物体的质量.
时,求所挂物体的质量.
如图,  是
是  的中点,
的中点,  是
是  的中点.
的中点.
 是
是  的中点,
的中点,  是
是  的中点.
的中点. ![]()
-
(1) 若
 ,则
,则 
 ;
;
-
(2) 若
 ,则
,则 
 ;
;
-
(3) 若
 ,则
,则 
 .
.
计算:(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2 .
下图是由六个相同正方体堆成的物体的图形,则这一物体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,将图形(1)以点O为旋转中心,每次顺时针旋转90°,则第2015次旋转后的图形是.
(在下列各图中选填正确图形的序号即可)

如图,在半圆O中,直径AE=10,四边形ABCD是平行四边形,且顶点A、B、C在半圆上,点D在直径AE上,连接CE,若AD=8,则CE长为 .

如果练习本每本a元,铅笔每支b元,那么3a+5b表示 .
已知![]() 是方程组
是方程组![]() 的解,则
的解,则![]() 、
、![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
)画出右边实物的三视图.

最近更新
- 用1、2、3、4、5、6组成一个无重复数字的六位数,要求三个奇数1、3、5有且只有两个相邻,则不同的排法种数为
- .下图体现了汉字的演变历程。影响汉字演变的主要因素有: ①印刷技术的进步 ②书写工具的改进
- 在相同状况下,有关H2、O2、CH4三种气体的叙述正确的是( ) A.其
- ......
- 植物从土壤中吸收的氮素,可用于合成 A.淀粉、蛋白质 B.蔗糖、氨基酸 C.葡萄糖、纤维素
- 在80℃时,将0.4 mol的四氧化二氮气体充入2L已抽空的固定容积的密闭容器中,隔一段时间对该容器内的物质进行分析,得
- 2013年中央一号文件提出,鼓励和支持承包土地向专业大户、家庭农场、农民合作社流转。其中,“家庭农场”概念首次在中央一号
- Whenmiddle-aged Alex quit his job and made up his mind
- 右图为实验鼠肝脏细胞亚显微结构模式图,请据图回答下列问题:(1)该细胞如果能连续分裂,则处于细胞周期的 期。该时
- “综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的
- 下列加点的字,每对读音都不相同的一组是( ) A.遒劲/疾风劲草 负荷/荷枪实弹 蹊跷/独辟蹊径 B.
- 如图所示,在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场。一个不计重力的带电粒子从坐标原点O处以速度v进入磁场
- —That actor often joins in dfferent activities in Beijing. D
- 某化学学习小组对铝与酸和碱的反应进行探究,过程如下。实验I:(1)取形状、大小均相同的铝丝分别与等体积的、PH相同的盐酸
- 袋装食品中常用一种“双吸剂”保质,主要成分是铁粉和生石灰,同学们对一久置的双吸剂固体样品很好奇,设计了如下实验进行探究。
- 2006年美国《思想之林》杂志评选“十大人类有史以来最伟大的国家”,意大利以头名入选。根据所学的历史知识判断,其入选依据
- 已知下列函数中是周期函数且最小正周期为的是 A. B. C. D.
- 阅读下面的作品,完成小题。正则艺专高尔泰(1)宁沪线上位于镇江和无锡之间的丹阳市, 是一座毫无特色的小城;正则艺专所在的
- 我国纬度最高和最低的省区是( ) A、黑和粤 B、黑和琼 C、新和台
- Later they discovered, ____ was news to him, that Pamela was



