初中 数学
计算:
-
(1) 5
 +
+ 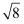 ﹣7
﹣7 
-
(2)
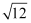 ×(
×(  +3
+3 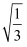 ﹣
﹣ 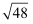 )
)
为了帮助我市一名贫困学生,某校组织捐款,现从全校所有学生的捐款数额中随机抽取10名学生的捐款数统计如下表:
| 捐款金额/元 | 20 | 30 | 50 | 90 |
| 人数 | 2 | 4 | 3 | 1 |
则下列说法正确是( )
A . 10名学生是总体的一个样本
B . 中位数是40
C . 众数是90
D . 方差是400
观察下列计算
 =1﹣
=1﹣  ,
,  =
=  ,
,  =
=  -
-  ,
,  =
=  ﹣
﹣  …
…
-
(1) 第5个式子是;第n个式子是.
-
(2) 从计算结果中找规律,利用规律计算.
 +
+  +…+
+…+ 
-
(3) 计算
 +…+
+…+ 
-
(4) 计算
 +
+  +…+
+…+ 
不等式组  的解集是.
的解集是.
 的解集是.
的解集是.
如图,在▱ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.
求证:BC=BF.

若y=(a+2)x2-3x+2是二次函数,则a的取值范围是( )
A . a≠0
B . a>0
C . a>2
D . a≠-2
第七次人口普查显示,高安市常住人口约为740000人,将数据740000用科学记数法表示为( )
A . 74×104
B . 7.4×105
C . 0.74×106
D . 7.4×107
下列运算中正确的是( )
A . (x3)2=x5
B . 2a﹣5•a3=2a8
C .  D . 6x3÷(﹣3x2)=2x
D . 6x3÷(﹣3x2)=2x
 D . 6x3÷(﹣3x2)=2x
D . 6x3÷(﹣3x2)=2x
方程8x3+1=0的根是.
如图,AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的度数是( )

A . 65°
B . 60°
C . 55°
D . 50°
如图,平面直角坐标系中,A(﹣3,0)B(0,4)把△AOB按如图标记的方式连续做旋转变换,这样得到的第2017个三角形中,O点的对应点的坐标为.

如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.

-
(1) 当t为何值时,四边形ABDE是矩形;
-
(2) 当t为何值时,四边形OEDC是平行四边形?
-
(3) 连接AD,记△ADE的面积为S,求S与t的函数关系式.
如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1 , B1 , C1 , 使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 , 记其面积为S1;第二次操作,分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使得A2B1=2A1B1 , B2C1=2B1C1 , C2A1=2C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , 记其面积为S2 , 则S2=。

如图,点  为菱形
为菱形  边上的一个动点,并沿
边上的一个动点,并沿  →
→  →
→  →
→  的路径移动,设点E经过的路径长为
的路径移动,设点E经过的路径长为  ,
, 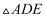 的面积为
的面积为  ,则下列图象能大致反映
,则下列图象能大致反映  与
与  的函数关系的是( )
的函数关系的是( )
 为菱形
为菱形  边上的一个动点,并沿
边上的一个动点,并沿  →
→  →
→  →
→  的路径移动,设点E经过的路径长为
的路径移动,设点E经过的路径长为  ,
, 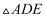 的面积为
的面积为  ,则下列图象能大致反映
,则下列图象能大致反映  与
与  的函数关系的是( )
的函数关系的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知|x|=5,|y|=3.
-
(1) 若x>y,求x+y的值.
-
(2) 若xy<0,求|x-y|的值.
点P在线段AB的垂直平分线上,PA=10,则PB=______.
如图,正方形![]() ABCD中,AB=
ABCD中,AB=![]() ,延长BC至E,使BE=BD,则△BDE的面积为 。
,延长BC至E,使BE=BD,则△BDE的面积为 。

若一组数据3,-1,0,2,x的极差是5,则x=______.
计算:![]() ;
;
根据给出的数轴及已知条件,解答下面的问题:
![]()
![]()
(1)已知点A,B,C表示的数分别为1,﹣![]()
![]() ,﹣3观察数轴,与点A的距离为3的点表示的数是 ,B,C两点之间的距离为 ;
,﹣3观察数轴,与点A的距离为3的点表示的数是 ,B,C两点之间的距离为 ;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M ,N ;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P ,Q (用含m,n的式子表示这两个数).
最近更新
- 现有A、B、C三种化合物,各取40g相混合,完全反应后,得到18.0g B、49.0g C、还有D生成,已知D的式量为1
- John McCain and Barack Obama call for closer U.S.-Chinese co
- 能完整地体现五四运动所反映历史事件性质的口号是( ) A.“废除二十一条” B.“拒绝在
- 选出没有错别字的一项( )(2分)A.花枝招展 一泄千里 姿态万千 慷概淋漓B.红妆素裹
- 若,则m的范围是 ( )A.1 <
- 按照题目要求作图. (1)在左图中的〇里填上适当的电表符号,闭合电键S使L1和L2两灯都能同时发光。 (2)磁体旁小磁针
- “米猪肉”是指含有什么的猪肉:A、米粒 B、猪肉绦虫卵 C、猪肉绦虫幼虫 D、猪肉绦虫成虫
- 今年的6月5日是第44个“世界环境日”,也是我国新《环保法》实施后的首个“环境日”.我国今年的主题是“践行绿色生活”,下
- 汽车安全气囊内的物质,在碰撞瞬间能生成一种空气中体积含量最多的气体,该气体是 A.氮气 B.氧气 C.稀
- 1936年12月12日张学良、杨虎城扣押在西安督战的蒋介石,发动震惊全国的西安事变。他们的做法反映了全国上下: A.主张
- 2009年全国财政赤字拟安排合计为9500亿元。根据统计,这一赤字规模创出了新中国60年的最高纪录,是历史高值的2003
- 化学家们合成了如下图所示的一系列的星烷,如三星烷、四星烷、五星烷等。下列说法正确的是( ) A.它们之间互为同系物
- 阅读下面的文字,完成后面题目。 锁 王 下岗前,陈锁锁最大的爱好就是收藏锁,各种各样的锁摆满了一间房子,人们戏称他“锁王
- 分布在亚洲东部的主要人种是:A.白种人B.黄种人C.黑种人D.混血种人
- 已知有机物 A、B、C、D、E、F之间的转化关系如图所示。D 是常用做汽车发动机的抗冻剂,E为聚合物,F的式量为26。根
- 为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌
- (14分)近年来,碳和碳的化合物在生产生活实际中应用广泛。(1)甲烷燃烧放出大量的热,可作为能源用于人类的生产和生活。已
- 如图,直线与x轴、y分别相交与A、B两点,圆心P的坐标为(1,0),圆P与y轴相切与点O.若将圆P沿x轴向左移动,当圆P
- 反应①②分别是从海藻灰和某种矿石中提取碘的主要反应: ①2NaI+MnO2+3H2SO4=2NaHSO4+MnSO4+2
- 淮安市某盐化厂生产的碳酸钠粗产品中含有少量氯化钠.碳酸钠和氯化钠的溶解度与温度的关系如图所示,回答下列问题: (1)t1



