初中 数学
sin70°,cos70°,tan70°的大小关系是( )
A . tan70°<cos70°<sin70°
B . cos70°<tan70°<sin70°
C . sin70°<cos70°<tan70°
D . cos70°<sin70°<tan70°
列方程解应用题
《九章算术》中有“盈不足术”的问题,原文如下:“今有共買羊,人出五,不足四十五;人出七,不足三.问人数、羊價各幾何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元.求人数和羊价各是多少?
已知a,b,c是△ABC的三边,且满足关系式a2+c2=2ab+2bc﹣2b2 , 试判断△ABC的形状.
如果a与-2的和为0,那么a是( )
A . 2
B .  C . -
C . - D . -2
D . -2
 C . -
C . - D . -2
D . -2
如图,在⊙O中,AC为⊙O直径,B为圆上一点,若∠OBC=26°,则∠AOB的度数为( )

A . 26°
B . 52°
C . 54°
D . 56°
若  ,则
,则  的值为( )
的值为( )
 ,则
,则  的值为( )
的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在矩形纸片 中,
中, ,
,  . 将矩形纸片沿
. 将矩形纸片沿 折叠,使点B与D重合.有下列语句:①四边形
折叠,使点B与D重合.有下列语句:①四边形 是菱形;②
是菱形;② ;③
;③ ;④
;④ . 其中正确的有( )
. 其中正确的有( )
 中,
中, ,
,  . 将矩形纸片沿
. 将矩形纸片沿 折叠,使点B与D重合.有下列语句:①四边形
折叠,使点B与D重合.有下列语句:①四边形 是菱形;②
是菱形;② ;③
;③ ;④
;④ . 其中正确的有( )
. 其中正确的有( )
A .  个
B .
个
B .  个
C .
个
C .  个
D .
个
D .  个
个
 个
B .
个
B .  个
C .
个
C .  个
D .
个
D .  个
个
小华进行了5次射击训练后,计算出这5次射击的平均成绩为8环,方差为s12 , 随后小华又进行了第6次射击,成绩恰好是8环,并计算出这6次射击成绩的方差为s22 , 则下列说法正确的是( )
A . s12=s22
B . s12<s22
C . s12>s22
D . 无法确定s12与s22的大小
如图,∠MAN=65°,进行如下操作:以射线AM上一点B为圆心,线段BA长为半径作弧,交射线AN于点C,连接BC,则∠BCN的度数是( )

A . 55°
B . 65°
C . 115°
D . 130°
有理数的计算:
-
(1) ﹣14+16÷(﹣2)3×|﹣3﹣1|
-
(2) (﹣
 +
+ 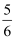 ﹣
﹣ 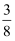 )×(﹣24).
)×(﹣24).
下列计算正确的是( )
A . (﹣3a)2=﹣9a2
B .  =﹣1
C . 2a2﹣1=(2a+1)(2a﹣1)
D . a3﹣4a3=﹣3a3
=﹣1
C . 2a2﹣1=(2a+1)(2a﹣1)
D . a3﹣4a3=﹣3a3
 =﹣1
C . 2a2﹣1=(2a+1)(2a﹣1)
D . a3﹣4a3=﹣3a3
=﹣1
C . 2a2﹣1=(2a+1)(2a﹣1)
D . a3﹣4a3=﹣3a3
先化简,再求值
-
(1) 已知
 ,
,  ,求
,求  的值,其中
的值,其中  ,
, 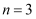 .
.
-
(2) 若
 ,
, 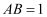 ,求
,求  的值.
的值.
中央电视台的“中国诗词大赛”节目文化品位高,内容丰富.某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

-
(1) 扇形统计图中“优秀”所对应扇形的圆心角为度,并将条形统计图补充完整.
-
(2) 此次比赛有四名同学获得满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
如图,矩形ABCD对角线相交于点O,∠AOB=60°,AB=4,则矩形的边AC为( )

A . 4
B . 8
C . 4  D . 10
D . 10
 D . 10
D . 10
四边形ABCD的两条对角线将这个四边形分为四个全等的等腰直角三角形,那么此四边形一定是( )
A . 正方形
B . 菱形
C . 矩形
D . 平行四边形
如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )

A . 180°
B . 360°
C . 270°
D . 540°
化简  的结果是()
的结果是()
 的结果是()
的结果是()
A .  B .
B .  C .
C . 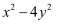 D .
D . 
 B .
B .  C .
C . 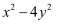 D .
D . 
点  点在第四象限,且点
点在第四象限,且点  到
到  轴、
轴、  轴的距离分别为6、8,则点
轴的距离分别为6、8,则点  的坐标为.
的坐标为.
 点在第四象限,且点
点在第四象限,且点  到
到  轴、
轴、  轴的距离分别为6、8,则点
轴的距离分别为6、8,则点  的坐标为.
的坐标为.
要使代数式![]() 有意义,则
有意义,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( )
A. B.
B. C.
C. D.
D.
最近更新
- 洪灾过后,饮用水的消毒杀菌成为抑制大规模传染性疾病爆发的有效方法之一。漂白粉是常用的消毒剂。工业上将氯气通入石灰乳[Ca
- 组成玉米和人体的最基本元素是 ( ) A.氢元素 B.氧元素 C.氮元素 D.碳元素
- 风洞是对飞机、导弹性能进行检测的一种高科技产物,现代汽车的生产也有运用风洞技术进行检测的,如图所示是小英所在兴趣小组设计
- 某化学实验活动小组的同学为了探究实验室中久置的氢氧化钠固体的成分,进行了有关实验.请你参与他们进行的探究活动: 【提出问
- I am calling to inquire about the position _____ in yesterda
- 有关电解水实验(如图)的下列叙述,正确的是()A.水是由氢分子和氧分子构成的 B.水是由氢原子和氧原子构成的 C.试管甲
- 将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同。甲从袋中摸出一个球,其号码为a,放回
- 秦始皇、汉武帝在处理哪一方面问题时态度截然相反( ) A.国家统一 B.中央集权 C.儒
- 用芳香烃A为原料合成G的路线如下: 其中D分子苯环上只有一个支链,该分子在光照条件下与Cl2 发生取代
- 汽车在平直公路上以速度v0匀速行驶,发动机功率为P。快进入闹市区时,司机减小了油门,使汽车的功率立即减小一半并保持该功率
- 铝、铁、铜是我们生活中常见的金属. (1)铝制品具有很好的耐腐蚀性能,原因是(2)为探究铝、铁、铜三种金属的活动性顺序,
- 阅读理解 阅读下面材料,从每题所给的A、B、C、D四个选项中选出最佳选项。 I am off on a t
- 阅读下面材料,按要求答题。(共10分) 中新网消息:教育部语用司日前在全国七个省(市)进行的有关语文 学习特别是汉字 书
- The Man of Many Secrets — Harry Houdini — was one of the gre
- 若一艘油轮在美国东部沿海附近发生严重泄漏,下列地区受污染最严重的是 A.西欧沿海 B.墨西哥东部沿海 C.加拿大西北部
- 将18.0 mol·L-1的浓硫酸稀释成2.00 mol·L-1的稀硫酸100 mL,实验操作如下,请并填写有关空格:
- 下列叙述中符合安全用电原则的是( ▲ ) A.用测电笔辨别火线、零线时,手一定要接触笔尖金属体 B.在家庭电路中增添大功
- 电子计算机又被通俗地称为“电脑”,其原因是( ) A.能节省劳力,提高生产率 B.具有人脑部分功能,能进行脑力劳动
- 下列有关生活和环境问题的一些说法正确的是( ) ①加碘盐中“碘”通常是碘酸钾 ②使用含磷洗涤剂后的废水不经处理直
- One day I a newspaper article about the retirement of



