初中 数学

 B .
B .  C .
C .  D .
D . 

 B . 2
B . 2  C .
C .  D .
D . 

-
(1) 写出点A表示的数的相反数和点B表示的数的绝对值
-
(2) 将点A先向右移动1.5个单位长度,再向左移动5个单位长度,得到点C,在数轴上表示出点C,并写出点C表示的数.
 的坐标为
的坐标为  ,且点
,且点  到
到  轴的距离是1,则点
轴的距离是1,则点  的坐标是.
的坐标是.
已知,抛物线y=ax²+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.

-
(1) 求抛物线的解析式;
-
(2) 如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
-
(3) 如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线
 对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
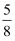 B .
B .  C .
C .  D .
D . 
 ,∠B=60°,OD⊥AC,垂足为D.
,∠B=60°,OD⊥AC,垂足为D.
-
(1) 求OD的长;
-
(2) 求劣弧AC的长.
 ,
,  ,
,  是实数,则下列判断正确的是( )
是实数,则下列判断正确的是( )
 ,则
,则  B .
B .  C . 若
C . 若  ,则
,则  D . 若
D . 若  ,则
,则 

-
(1) 试说明△BAD≌△CAE;
-
(2) 若DE=DC , 求∠CDE的度数.
 .
.
 的对称轴是直线( )
的对称轴是直线( )
 B .
B . 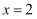 C .
C . 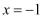 D .
D . 

①长方体、直六棱柱、圆锥都是多面体;
②腰相等的两个等腰三角形全等;
③有一边及一锐角对应相等的两个直角三角形全等;
④两直角边长为8和15的直角三角形,斜边上的中线长9;
⑤三角之比为3:4:5的三角形是直角三角形

第一档电量 | 第二档电量 | 第三档电量 |
月用电量210度以下,每度价格0.52元 | 月用电量210度至350度,每度比第一档提价0.05元 | 月用电量350度以上,每度比第一档提价0.30元 |
例:若某户月用电量400度,则需交电费为210×0.52+(350﹣210)×(0.52+0.05)+(400﹣350)×(0.52+0.30)=230(元)
-
(1) 如果按此方案计算,小华家5月份的电费为138.84元,请你求出小华家5月份的用电量;
-
(2) 以此方案请你回答:若小华家某月的电费为a元,则小华家该月用电量属于第几档?
(1)3.6×107﹣1.2×106; (2)36×(-3 )4×100.
)4×100.
先化简,再求值:(2x2+3x)﹣2(2x﹣1+x2),其中x=﹣![]() .
.
课本再现
( 1 )在证明 “ 三角形内角和定理 ” 时,小明只撕下三角形纸片的一个角拼成图 1 即可证明,其中与 相等的角是 ______ ;

类比迁移
( 2 )如图 2 ,在四边形 中,
与
互余,小明发现四边形
中这对互余的角可类比( 1 )中思路进行拼合:先作
,再过点


,连接

,
,

方法运用

( 3 )如图 3 ,在四边形 中,连接


是
两边垂直平分线的交点,连接


① 求证: 
② 连接 
,

,求

,
的式子表示).
- 在右图食物网中,a表示鸟的能量中动物性食物所占比例,若要使鸟体重增加x,至少需要生产者量为y,那么x与y的关系可表示为(
- A、B两质点沿同一直线从同一地点出发,其运动情况在图中由A、B两条图线表示,下列说法正确的是 ( ) A.A、B同
- 如图所示,沿光滑的竖直墙壁用网兜把一个足球挂在A点。当悬线变短时,下列说法中正确的是( )A.悬线的拉力变小
- 设. (1)求函数的单调区间; (2)若当时恒成立,求的取值范围
- 物质的保存方法取决于物质的物理性质和化学性质。根据物质的性质判断下列各种物质的保存方法正确的是() A.浓硫酸保存
- 已知,则( 的值等于 _
- 以下命题中,正确命题的序号是: ①函数 不是周期函数 ②函数在定义域内是增函数 ③函数是偶函
- This morning Ms. Green entered our classroom, and _____ us s
- 中国下列交通和通信工具的进步与第二次工业革命有关的是() ①第一艘轮船 ②公共汽车运行 ③无线电报创设 A.①②
- 下图为东亚部分地区图,图中甲乙丙三地气候特征的差异最明显的表现是:( )①气温年较差②降水量的季节变化③夏季风风向和影
- 某学生的实验报告所列出的下列数据中合理的是 A.用10mL量筒量取7.13mL稀盐酸; B.用托盘天平
- 下列关于人体对甲型H1N1流感病毒免疫过程的说法,不正确的是 A.甲型H1N1流感病毒可以引起人体发生特异性免疫反应 B
- 工业上制备硝酸的尾气中,尚还有少量未被吸收的NO和NO2,如果不加处理就排放到空气中,会造成污染。为消除氮氧的化物对大气
- 在应对经济“新常态”过程中,我国加快推进协商民主广泛多层制度化发展,拓宽国家政权机关,政协组织、党派团体、基层组织、社会
- 计算:
- 已知多项式(2mx2-x2+3x+1)-(5x2-4y2+3x)化简后不含x2项. 求多项式2m3-[3m3-(4m-5
- 某社区近期举行了关于公民政治参与的交流活动,根据右面列举的政治现象,我们可以判断:①甲通过社情民意反映制度参与民主决策
- 下列植物中,被称为地球之“肺”的是A.针叶林 B.热带雨林 C草原 D.落叶阔叶林
- △ABC中,已知tanA=,tanB=,则∠C等于() A30°B45° C60°
- 阅读下面的内容,完成下面4题 大海的波涛是自然界最纯美、浑厚,且颇具神秘色彩的“音乐”。然而是谁“弹奏”了这一曲曲动人的



