初中 数学
据媒体报道,我国因环境污染造成的巨大经济损失,每年高达860 000 000元,这个数用科学记数法表示为元.
邮票素有“国家名片”之称,方寸之间,包罗万象.为宣传北京2022年冬奥会,中国邮政发行了若干套冬奥会纪念邮票,其中有一套展现雪上运动的邮票,如图所示:

某班级举行冬奥会有奖问答活动,答对的同学可以随机抽取邮票作为奖品.
-
(1) 在抢答环节中,若答对一题,可从4枚邮票中任意抽取1枚作为奖品,则恰好抽到“冬季两项”的概率是.
-
(2) 在抢答环节中,若答对两题,可从4枚邮票中任意抽取2枚作为奖品,请用列表或画树状图的方法,求恰好抽到“高山滑雪”和“自由式滑雪”的概率.
已知x、y、z满足  =
= 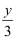 =
=  ,那么
,那么  =.
=.
 =
= 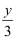 =
=  ,那么
,那么  =.
=.
世纪公园的门票是每人5元,一次购门票满40张,每张门票可少1元.若少于40人时,一个团队至少要有人进公园,买40张门反而合算.
某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
|
类型价格 |
A型 |
B型 |
|
进价(元/件) |
60 |
100 |
|
标价(元/件) |
100 |
160 |
-
(1) 请利用二元一次方程组求这两种服装各购进的件数;
-
(2) 如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
计算:
-
(1) (﹣1
 )﹣(+6
)﹣(+6  )﹣2.25+
)﹣2.25+ 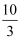 ;
;
-
(2) (﹣1)2021﹣|﹣8|+(﹣3)2﹣(
 ﹣
﹣  )×24.
)×24.
如图,已知长方形ABCD的长AB=x米,宽BC=y米,x,y满足|x-7|+(y-4)2=0,一动点P从A出发以每秒1米的速度沿着A→D→C→B运动,另一动点Q从B出发以每秒2米的速度沿B→C→D→A运动,P,Q同时出发,运动时间为t。

-
(1) x=,y=;
-
(2) 当t=4.5时,求△APQ的面积;
-
(3) 当P,Q都在DC上,且PQ距离为1时,求t的值。
若x﹣1= ,则代数式(x+1)2﹣4(x+1)+4的值为( )
,则代数式(x+1)2﹣4(x+1)+4的值为( )
 ,则代数式(x+1)2﹣4(x+1)+4的值为( )
,则代数式(x+1)2﹣4(x+1)+4的值为( )
A .  B . 5
C . 6+2
B . 5
C . 6+2 D . 6﹣2
D . 6﹣2
 B . 5
C . 6+2
B . 5
C . 6+2 D . 6﹣2
D . 6﹣2
如图,已知二次函数y=ax2+bx+c的图象经过A(2,0),B(0,﹣1)和C(4,5)三点.

-
(1) 求二次函数的解析式;
-
(2) 设二次函数的图象与x轴的另一个交点为D,求△BCD的面积.
-
(3) 在同一坐标系中画出直线y=x+1,并直接写出当x在什么范围内时,
一次函数的值小于二次函数的值.
在代数式  ,
,  ,
,  ,-5,a 中,单项式的个数是( )
,-5,a 中,单项式的个数是( )
 ,
,  ,
,  ,-5,a 中,单项式的个数是( )
,-5,a 中,单项式的个数是( )
A . 1个
B . 2个
C . 3个
D . 4个
如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把  的值称为⊙I关于直线a的“特征数”.
的值称为⊙I关于直线a的“特征数”.
 的值称为⊙I关于直线a的“特征数”.
的值称为⊙I关于直线a的“特征数”. 

-
(1) 如图2,在平面直角坐标系
 中,点E的坐标为
中,点E的坐标为  ,半径为1的⊙O与两坐标轴交于点A、B、C、D.
,半径为1的⊙O与两坐标轴交于点A、B、C、D. ①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点_▲__(填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为_▲__;
②若直线n的函数表达式为
 ,求
,求  关于直线n的“特征数”;
关于直线n的“特征数”; -
(2) 在平面直角坐标系
 中,直线l经过点
中,直线l经过点  ,点F是坐标平面内一点,以F为圆心,
,点F是坐标平面内一点,以F为圆心,  为半径作⊙F.若⊙F与直线l相离,点
为半径作⊙F.若⊙F与直线l相离,点  是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是
是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是  ,求直线l的函数表达式.
,求直线l的函数表达式.
如图,在△ABC中,AC=BC,⊙O是△ABC的外接圆,过点B作⊙的切线BD,连接AD交BC于点E,交⊙O于点F,连接BF.

-
(1) 求证:∠FBD=∠FAB;
-
(2) 若AE⊥BC,AC=6,
 ,求DF的长.
,求DF的长.
如果  是任意实数,则点P(
是任意实数,则点P(  ,
,  )一定不可能在( )
)一定不可能在( )
 是任意实数,则点P(
是任意实数,则点P(  ,
,  )一定不可能在( )
)一定不可能在( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
以下四个命题:①任意三角形的一条中位线与第三边上的中线互相平分;②A , B , C , D , E , F六个足球队进行单循环赛,若A , B , C , D , E分别赛了5,4,3,2,1场,则由此可知,还没有与B队比赛的球队可能是D队;③两个正六边形一定位似;④有13人参加捐款,其中小王的捐款数比13人捐款的平均数多2元,则小王的捐款数不可能最少,但可能只比最少的多.比其他的都少.其中真命题的个数有( )
A . 1个
B . 2个
C . 3个
D . 4个
若2x-3y=4,则多项式6y+1-4x的值是()
A . 7
B . 4
C . -7
D . -4
如图,二次函数  的图像经过
的图像经过  的三个顶点,其中
的三个顶点,其中  ,
, 
 的图像经过
的图像经过  的三个顶点,其中
的三个顶点,其中  ,
, 

-
(1) 求点A,B的坐标;
-
(2) 在第三象限存在点C,使以
 为顶点的四边形是平行四边形,求满足条件的点C的坐标;
为顶点的四边形是平行四边形,求满足条件的点C的坐标;
-
(3) 在(2)的条件下,能否将抛物线
 平移后经过
平移后经过  两点,若能求出平移后经过
两点,若能求出平移后经过  两点的拋物线的表达式,并写出平移过程.若不能,请说明理由.
两点的拋物线的表达式,并写出平移过程.若不能,请说明理由.
当 x =﹣ 2 时,分式 
A .﹣ 15 B .﹣ 3 C . 3 D . 15
4x2-49=0 ;
计算:![]() (4﹣
(4﹣![]() )0+[(2
)0+[(2![]() ﹣3)2]
﹣3)2]![]() .
.
下列各数中,最小的实数是( )
A.0 B.π C.﹣![]()
![]() D.﹣1
D.﹣1
最近更新
- 已知A物质是一种气态烷烃,标况下取22.4L该烃完全燃烧消耗氧气的质量是160g,A的一氯代物有两种同分异构体分别为B和
- --Can youcome to my party? ---_________. A,Sure ,I’d love
- 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点
- (21)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系用图一的一条折线
- 下列运输方式中,有“从门口到门口”的优势的是( ) A. 公路 B. 管道 C. 水路 D. 铁路
- 二次函数的图象如何移动就得到的图象 ( )A.向右移动1个单位,向上移动4个单位B.向左移动1个单位,向上
- 已知椭圆+=1(a>b>0)的左、右焦点分别为F1,F2,|F1F2|=2,点P为椭圆短轴的端点,且△PF1
- 11.对下列加横线词语文言词类活用判断,正确的一项是( ) ①伯杀人臣活之 ②籍吏民,封府库 ③使使以闻大王 ④謇朝
- 右图是著名漫画家钱病鹤先生于1909年创作的题为《各国联合龙灯大会》的漫画。对其表达的寓意表述正确的是 A. 反映了当时
- 22.Lawrence Craven, a doctor from the USA,is the author of s
- 在成人的乳腺细胞中比腹肌细胞数量显著多的细胞器是() A.核糖体 B. 线粒体
- 北京是我们国家的政治中心,向世界展示着中华文化的悠久与灿烂。回答问题。1.保护世界文化遗产的说法,正确的是( )
- 在空气中,与人类关系最密切的当属氧气。下列说法正确的是 A.带火星的木条在氧气中能够复燃,说明氧气能支持燃烧B.铁丝
- 下列词语中,加点的字读音全都正确的一组是 A.绚(xuàn)丽丰腴(yú)倩(qiàn)影乳臭(chòu)未干 B.赦(
- 20101年,我国首次加息。从2008年开始,我国实施从紧的货币政策,严格控制货币信贷总量和投放节奏.更好地调节社会总需
- 杜甫在《望岳》一诗中化用孔子名言“登泰山而小天下”的诗句是: ____ , _ 。
- 据史料记载,明太祖有一天问大臣:“天下谁人最快活?”有的人回答:“金榜题名者。”有的人回答:“功成名就者。”明太祖听了都
- (04年广东卷)若双曲线的焦点到它相应的准线的距离是2,则(A) (B)
- (2009上海初中物理知识竞赛复赛题)右图是水平公路上从车后看到的一辆行驶着的汽车的右后轮,根据图中所示现象可知:(
- In some parts of the world, tea with milk and sugar.



