初中 数学
已知α是锐角,若sinα=
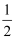 ,则α的度数是( )
,则α的度数是( )
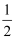 ,则α的度数是( )
,则α的度数是( )
A . 30°
B . 45°
C . 60°
D . 75°
如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
我们知道,  的重心就是三条中线
的重心就是三条中线  、
、  、
、 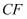 的交点G,如图1,其中
的交点G,如图1,其中  .如图2,
.如图2,  中,
中, 
 ,将
,将  绕其重心G旋转,A、B、C的对应点分别是
绕其重心G旋转,A、B、C的对应点分别是  、
、 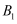 、
、  ,与
,与  的最大值最接近的是( )
的最大值最接近的是( )
 的重心就是三条中线
的重心就是三条中线  、
、  、
、 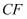 的交点G,如图1,其中
的交点G,如图1,其中  .如图2,
.如图2,  中,
中, 
 ,将
,将  绕其重心G旋转,A、B、C的对应点分别是
绕其重心G旋转,A、B、C的对应点分别是  、
、 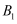 、
、  ,与
,与  的最大值最接近的是( )
的最大值最接近的是( )
(参考数据:  )
)


A . 5.5
B . 6.5
C . 7.5
D . 8.5
在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是.

关于  的一元二次方程
的一元二次方程  ,下列说法错误的是( )
,下列说法错误的是( )
 的一元二次方程
的一元二次方程  ,下列说法错误的是( )
,下列说法错误的是( )
A .  方程无实数解
B .
方程无实数解
B .  方程有一个实数解
C .
方程有一个实数解
C .  有两个相等的实数解
D .
有两个相等的实数解
D .  方程有两个不相等的实数解
方程有两个不相等的实数解
 方程无实数解
B .
方程无实数解
B .  方程有一个实数解
C .
方程有一个实数解
C .  有两个相等的实数解
D .
有两个相等的实数解
D .  方程有两个不相等的实数解
方程有两个不相等的实数解
过一个正多边形的某个顶点的所有对角线,将这个正多边形分成了4个三角形,则这个正多边形的每一个内角的度数是( )
A . 120°
B . 90°
C . 60°
D . 30°
若  是二次函数,则
是二次函数,则  的取值范围是( )
的取值范围是( )
 是二次函数,则
是二次函数,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,一次函数  与反比例函数
与反比例函数  的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
 与反比例函数
与反比例函数  的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点. 
-
(1) 求反比例函数的解析式;
-
(2) 求一次函数的解析式;
-
(3) 点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
如图,数轴上A、B两点分别对应有理数a、b,则下列结论:  ;
;  ;
;  ;
;  中正确的有
中正确的有 

 ;
;  ;
;  ;
;  中正确的有
中正确的有 

![]()
A . 1个
B . 2个
C . 3个
D . 4个
把角度化为度、分的形式,则20.5°=20°′;
小明在一次打篮球时,篮球传出后的运动路线为如图所示的抛物线,以小明所站立的位置为原点O建立平面直角坐标系,篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=- 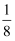 x2+x+c.
x2+x+c.
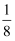 x2+x+c.
x2+x+c. 
-
(1) 求y与x之间的函数表达式;
-
(2) 球在运动的过程中离地面的最大高度;
-
(3) 小亮手举过头顶,跳起后的最大高度为BC=2.5m,若小亮要在篮球下落过程中接到球,求小亮离小明的最短距离OB.
在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为多少m?

下列说法不正确的是( )
A . 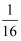 的平方根是
的平方根是  B . ﹣2是4的一个平方根
C . 0.2的算术平方根是0.04
D . ﹣27的立方根是﹣3
B . ﹣2是4的一个平方根
C . 0.2的算术平方根是0.04
D . ﹣27的立方根是﹣3
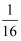 的平方根是
的平方根是  B . ﹣2是4的一个平方根
C . 0.2的算术平方根是0.04
D . ﹣27的立方根是﹣3
B . ﹣2是4的一个平方根
C . 0.2的算术平方根是0.04
D . ﹣27的立方根是﹣3
已知:如图,点A、B、C、D在同一直线上,BE∥CG,CG平分∠DCF,若∠1=50°,求∠ABE的度数.

综合与探究
在平面直角坐标系中,抛物线  经过点
经过点  ,点
,点  为抛物线的顶点,点
为抛物线的顶点,点  在
在  轴上,且
轴上,且  ,直线
,直线  与抛物线在第一象限交于点
与抛物线在第一象限交于点  ,如图.
,如图.

-
(1) 求抛物线的解析式;
-
(2) 直线
 的函数解析式为,点
的函数解析式为,点  的坐标为,
的坐标为,  .
.
-
(3) 在
 轴上找一点
轴上找一点  ,使得
,使得  的周长最小.请求出点
的周长最小.请求出点  的坐标;
的坐标;
-
(4) 在抛物线的对称轴上是否存在点
 ,使以点
,使以点  、
、  、
、  、
、  为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点  的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如果  能写成一个完全平方的形式,那么k等于;若
能写成一个完全平方的形式,那么k等于;若  ,那么a的值为.
,那么a的值为.
 能写成一个完全平方的形式,那么k等于;若
能写成一个完全平方的形式,那么k等于;若  ,那么a的值为.
,那么a的值为.
正整数排列如图:
第一行 1
第二行 1 2
第![]() 三行 2 3 4
三行 2 3 4
第四行 3 4 5 6
按照这样的规律排列,你认为100第一次出现在( )
A. 第50行第50个 B. 50行第![]() 51个 C. 第51行第50个 D. 第51行51个
51个 C. 第51行第50个 D. 第51行51个
如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=![]() 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.

如图,已知直线y=mx与双曲线y=![]()
![]() 的一个交点坐标为(3,4),则它们的另一个交点坐标是 .
的一个交点坐标为(3,4),则它们的另一个交点坐标是 .


有一组数据:2,5,5,6,7,这组数据的平均数为(C)
A.3 B.4
C.5 D.6
最近更新
- 下列加点字的读音有误的一组是 ( ) A.歆享
- 设,,,则的大小关系为( ) A. B. C. D.
- 下列说法错误的是 ( ) A. 三倍体无子西瓜的性状可以遗传,但它不是一
- 设函数f(x)=2+1(x∈R)的反函数为f -1(x),则函数y= f -1(x)的图象是 A
- 第三节 回答问题(共3小题;每小题2分,满分6分) 阅读下面短文,根据第58至第60小题的具体要求,简要回答问题,并将答
- “五十六个民族五十六枝花,五十六个兄弟姐妹是一家。”我国“五十六个兄弟姐妹”之所以是一家,其根本原因在于A.各民族之间有
- 分别比较下列两组句子中加点的字的意思,判断正确的一项( ) ①信乃使万人先行 ③且彼未见吾大将旗鼓
- 24.阅读下面的材料,根据要求作文。 有一棵大树,枝繁叶茂,浓荫匝地,是飞禽、走兽们喜爱的休息场所。飞禽、走兽们谈论着自
- (4分)某同学根据所学得光学知识,设计了一个测透明液体折射率得仪器,如图所示。在圆盘上作直径BC⊥EF,在半径OA上垂直
- 下列关于热学的知识叙述正确的是A.分子间的作用力表现为引力时,若分子间的距离增大,则分子力减小,分子势能增大 B.对于一
- 为了保证长时间潜航,在潜水艇里需配备氧气发生装置,有以下几种制取氧气的方法:①加热高锰酸钾;②电解水;③在常温下用过氧化
- 某小鼠的癌细胞具有氯霉素抗性,通过细胞核移植技术,将无氯霉素抗性的小鼠体细胞核取出,注入去核的小鼠癌细胞中,然后将这一重
- 太平天国是中国资产阶级民主革命的“准备阶段”,因为它( ) A、建立了与清政府对峙的政权 B、是中
- 下列有关基因工程的叙述,正确的是 A.DNA连接酶的作用是将两个黏性末端的碱基连接起来 B.目的基因导入受体细胞后,受体
- 积土成山,风雨兴焉。积水成渊,蛟龙生焉。积善成德,而神明自得,圣心备焉。故不积跬步无以至千里不积小流无以成江海骐骥一跃,
- 有关细胞结构和功能的叙述,正确的是() A.能进行有氧呼吸的细胞一定有线粒体 B.细胞核是细胞遗传和代谢活动的控制中心
- 已知是椭圆上关于原点对称的两点,是椭圆上任意一点,且直线的斜率分别为,若的最小值为,则椭圆的离心率为
- 一次参观活动中,一位同学看到一个零件的三视图都相同,那么该零件的实际形状可能是 (请写出2种)
- 阅读下面这首诗 雨过山村 王建 雨里鸡鸣一两家,竹溪村路板桥斜。妇姑相唤浴蚕去,闲看中庭栀子花。 1阅读全诗,
- 已知铁的比热容小于铝的比热容。质量相同的铁块和铝块吸收相同的热量后,_______温度升高的多;若它们降低相同的温度,_



