初中 数学
下列各式,去括号正确的是( )
A . a+(b﹣c)+d=a﹣b+c﹣d
B . a﹣(b﹣c+d)=a﹣b﹣c+d
C . a﹣(b﹣c+d)=a﹣b+c﹣d
D . a﹣(b﹣c+d)=a﹣b+c+d
下列防控疫情的图标中,既是轴对称图形,又是中心对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图1,在 中,
中, , AB是
, AB是 的直径,
的直径, 交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是
交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是 的切线.
的切线.
 中,
中, , AB是
, AB是 的直径,
的直径, 交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是
交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是 的切线.
的切线. 
-
(1) 求证:
 ;
;
-
(2) 若
 ,
,  , 求图中阴影部分的周长和面积;
, 求图中阴影部分的周长和面积;
-
(3) 如图2,
 , 连接DM,交AB于点N,若
, 连接DM,交AB于点N,若 , 求
, 求 的值.
的值. 
抛物线y=﹣2x2+4的顶点坐标为( )
A . (4,0)
B . (0,4)
C . (4,2)
D . (4,﹣2)
抛物线y=x2﹣6x+5向上平移3个单位长度,再向左平移2个单位长度后,得到的抛物线解析式是.
按如图所示的程序计算,若开始输入的n值为  ,则最后输出的结果是
,则最后输出的结果是
 ,则最后输出的结果是
,则最后输出的结果是 ![]()
利用等式的性质解方程: 5﹣x=﹣2
5的绝对值是( )
A . 5
B . 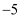 C .
C .  D .
D . 
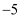 C .
C .  D .
D . 
下列图形中,是轴对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列说法正确的是( )
A . 全等三角形是指形状相同的两个三角形
B . 全等三角形是指面积相等的两个三角形
C . 两个等边三角形是全等三角形
D . 全等三角形是指两个能完全重合的三角形
在平面直角坐标系中,对于点P(a , b),我们把Q(﹣b+1,a+1)叫做点P的伴随点,已知A1的伴随点为A2 , A2的伴随点为A3 , …,这样依次下去得到A1 , A2 , A3 , …,An , 若A1的坐标为(3,1),则A2018的坐标为.
深圳市某公司自主设计了一款可控温杯,每个生产成本为18元,投放市场进行了试销.经过调查得到每月销售量y(万个)与销售单价x(元/个)之间关系是一次函数的关系,部分数据如下:
销售单价x(元/个) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万个) | … | 60 | 50 | 40 | 30 | … |
-
(1) 求y与x之间的函数关系;
-
(2) 该公司既要获得一定利润,又要符合相关部门规定(一件产品的利润率不得高于50%)请你帮助分析,公司销售单价定为多少时可获利最大?并求出最大利润.
下列实际问题中,可以看作二次函数模型的有( )
①正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数b与这个人的年龄a之间的关系为b=0.8(220-a);②圆锥的高为h,它的体积V与底面半径r之间的关系为V=  πr2h(h为定值);③物体自由下落时,下落高度h与下落时间t之间的关系为h=
πr2h(h为定值);③物体自由下落时,下落高度h与下落时间t之间的关系为h=  gt2(g为定值);④导线的电阻为R,当导线中有电流通过时,单位时间所产生的热量Q与电流I之间的关系为Q=RI2(R为定值).
gt2(g为定值);④导线的电阻为R,当导线中有电流通过时,单位时间所产生的热量Q与电流I之间的关系为Q=RI2(R为定值).
A . 1个
B . 2个
C . 3个
D . 4个
把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A . y=-x2+50x
B . y=x2-50x
C . y=-x2+25x
D . y=-2x2+25
四张完全相同的卡片上,分别画有圆、矩形、等边三角形、等腰梯形,现从中随机抽取一张,卡片上画的恰好是轴对称图形的概率为( )
A .  B .
B .  C .
C .  D . 1
D . 1
 B .
B .  C .
C .  D . 1
D . 1
若a>b,则下列四个不等式中正确的是( )
A . 3a>3b
B . a+5<b+5
C . -5a>-5b
D . a-2<b-2
如图,二次函数 图象的对称轴为直线
图象的对称轴为直线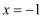 , 下列结论中,其中结论正确的是( ).
, 下列结论中,其中结论正确的是( ).
 图象的对称轴为直线
图象的对称轴为直线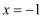 , 下列结论中,其中结论正确的是( ).
, 下列结论中,其中结论正确的是( ).① ;②
;② ;③
;③ ;④若m为任意实数,则有
;④若m为任意实数,则有 ;
;
⑤若图象经过点 , 方程
, 方程 的两根为
的两根为 ,
,  , 则
, 则 .
.

A . ①②③
B . ②③④
C . ②③⑤
D . ③④⑤
如图,点A在反比例函数  (x>0)的图象上,点B在反比例函数
(x>0)的图象上,点B在反比例函数  的图象上,AB⊥x轴于点M,且AM:MB=1:2,则k的值为( )
的图象上,AB⊥x轴于点M,且AM:MB=1:2,则k的值为( )

A . 3
B . ﹣6
C . 2
D . 6
如图△OAB绕点O逆时针旋转90°到△OCD的位置,已知∠AOB=45°,则∠AOD的度数为 ( ).
(A)55° (B)45° (C)40° (D)35°

如图所示,![]() 下列条件中,不能判断
下列条件中,不能判断![]() 的是( )
的是( )
A.AB=DE![]() B.
B.![]() ∠B=∠E C.EF=B
∠B=∠E C.EF=B![]() C D.EF∥BC
C D.EF∥BC

最近更新
- 一渔民承包一鱼塘,他应怎样合理利用池塘生态系统( ) A.禁渔三年
- 地球自转的真正周期是一个恒星日,即以太阳这颗恒星为参考点的周期。 ( )
- 外力作用的能量主要来自( ) A.太阳辐射能 B.重力能 C.地热能 D.核能
- “蜜蜂传粉”和“蜻蜓点水”这两种昆虫行为分别属于 ( ) A.防御行为和取食行为 B.防御行为和迁徙行为 C.取食
- 蛋白质、DNA和RNA的基本组成单位依次是( ) A.脱氧核苷酸、核苷酸、核糖核苷酸 B.核苷酸、脱氧核苷酸
- 某同学通过查找资料自己动手制作了一个电池。该同学想测量一下这个电池的电动势E 和内电阻,但是从实验室只借到一个开关、一个
- 下列哪个选项的长度是33dm A. 教室每层楼高 B. 一张纸的厚度 C. 课桌高度 D.一位中学生的
- 某同学在探究“物体的质量跟体积的关系” 的实验中,(1)他将托盘天平放在水平桌面上,把游码移到标尺左端的“0”刻度线处,
- 某密闭容器内盛有氧气和氮气的混合气体,采用燃烧法除去其中的氧气,且不能混入新的气体,最好采用的可燃物是( ) A
- 若点P到定点F(4,0)的距离比它到直线x+5=0的距离小1,则点P的轨迹方程是()A.y2=-16x
- 函数的部分图象如图所示, 若,且 ,则 A. B.
- 某化学兴趣小组欲测定某石灰石样品中碳酸钙的质量分数。取20g石灰石样品(假设杂质既不溶于水,也不与其他物质反应),向其中
- 有些同学放学时骑自行车行驶太快,容易造成交通事故,这是因为: A.运动快所以惯性大,因此难停下来 B.刹车时产生的惯性不
- (6分)下图所示各物质是由短周期部分元素组成的单质或其化合物,图中部分反应条件及物质未列出。已知:A、C、D、F均为单
- 物体静止在水平桌面上,物体对水平桌面的压力 A.就是物体的重力
- I’m full now, would you like ________ bread?A. one more
- 江畔独步寻花 (5分) 黄四娘家花满蹊,千朵万朵压枝低。 留连戏蝶时时舞,自在娇莺恰恰啼。【小题1】、
- 25. 阅读下面的文字,根据要求写一篇不少于800字的文章。 玫瑰说:“我只有在春天开花!” 长春花说:“我开花的每一天
- 下列各旬中加点的成语,使用不恰当的一项是( ) A、紫砂杯具自古以来就为茶器之首,其丰厚的文化底蕴与保健功效
- 巴尔扎克《欧也尼葛朗台》中老葛朗台的性格特征是什么?举出一二个细节说明。



