初中 数学
如图等边三角形  内接于
内接于  ,若
,若  的半径为1,则图中阴影部分的面积等于.
的半径为1,则图中阴影部分的面积等于.
 内接于
内接于  ,若
,若  的半径为1,则图中阴影部分的面积等于.
的半径为1,则图中阴影部分的面积等于. 
计算
-
(1) ﹣2a•
 ab2•(2ab3c)2;
ab2•(2ab3c)2;
-
(2) (﹣4a﹣3b)2 .
给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.

∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A . ②①①
B . ②①②
C . ①②②
D . ①②①
近年来,华为手机越来越受到消费者的青睐.截至2019年12月底,华为5G手机全球总发货量突破690万台.将690万用科学记数法表示为( )
A . 0.69×107
B . 69×105
C . 6.9×105
D . 6.9×106
方程组  有正整数解,则k的正整数值是( )
有正整数解,则k的正整数值是( )
 有正整数解,则k的正整数值是( )
有正整数解,则k的正整数值是( )
A . 3
B . 2
C . 1
D . 不存在
对单项式“0.8a”可以解释为:一件商品原价为a元,若按原价的8折出售,这件商品现在的售价是0.8a元,请你对“0.8a”再赋予一个含义:
下列图形中既是中心对称图形又是轴对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.

-
(1) 直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示)
-
(2) 点E是直线l上方的抛物线上的一点,若△ACE的面积的最大值为
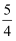 , 求a的值;
, 求a的值;
-
(3) 设P是抛物线对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
如图,O是直线AB上一点,∠AOC=50°,则∠BOC的度数是( )

A . 120°
B . 130°
C . 140°
D . 150°
如图放置的一个圆锥,它的主视图是直角边长为2的等腰直角三角形,则该圆锥侧面展开扇形的弧长为.(结果保留π)
![]()
如果关于  的不等式组
的不等式组  的解集为
的解集为  ,且整数
,且整数  使得关于
使得关于 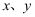 的二元一次方程组
的二元一次方程组  的解为整数(
的解为整数( 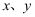 均为整数),则符合条件的所有整数
均为整数),则符合条件的所有整数  的和是( )
的和是( )
 的不等式组
的不等式组  的解集为
的解集为  ,且整数
,且整数  使得关于
使得关于 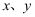 的二元一次方程组
的二元一次方程组  的解为整数(
的解为整数( 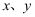 均为整数),则符合条件的所有整数
均为整数),则符合条件的所有整数  的和是( )
的和是( )
A . 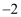 B . 2
C . 6
D . 10
B . 2
C . 6
D . 10
 B . 2
C . 6
D . 10
B . 2
C . 6
D . 10
下列函数中是二次函数的是( )
A . y=  B . y=(x+3)2﹣x2
C . y=
B . y=(x+3)2﹣x2
C . y=  D . y=x(x﹣1)
D . y=x(x﹣1)
 B . y=(x+3)2﹣x2
C . y=
B . y=(x+3)2﹣x2
C . y=  D . y=x(x﹣1)
D . y=x(x﹣1)
在△ABC中,AB=3,AC=4,BC=5,点P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )
A . 2.5
B . 2.4
C . 2.2
D . 2
如图,将三角板的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3=°.

下面四个图形中不是轴对称图形的是( )
A . 
B .
B . 
C .
C . 
D .
D . 

B .
B . 
C .
C . 
D .
D . 
一个含30°角和另一个含45°角的三角板按如图所示放置,直角顶点重合,且两条斜边  ,则
,则  °.
°.
 ,则
,则  °.
°. 
甲、乙两个工程队修筑一段长为300米的公路,如果甲、乙两队从公路两端相向施工,已知乙工程队修筑的公路比甲工程队修筑的公路的2倍少20米,求该工程完工后甲、乙两个工程队分别修筑了多少米公路?
已知⊙O中,AC为直径,DA、DB分别切⊙O于点A、B.
(Ⅰ)如图①,若∠D=50°,求∠C的大小;
(Ⅱ)如图②,过点B作BE⊥AC于点F,交⊙O于点E,若BD=BE,求∠C的大小.

已知⊙O的半径为4cm,点P到圆心O的距离为3cm,则点P( )
| A.在圆内 | B.在圆上 | C.在圆外 | D.不能确定 |
下列方程是一元二次方程的是( )
A.ax2+bx+c=0 B.x2+2x=x2﹣1 C.(x﹣1)(x﹣3)=0 D.![]()
![]() =2
=2
最近更新
- 孟德尔遗传定律的研究、萨顿关于基因与染色体关系的研究,所运用的方法分别是 A.类比推理法、假说演绎法
- 近年来“金砖四国”(巴西、俄罗斯、印度和中国)和“远景五国”(越南、印度尼西亚、南非、土耳其和阿根廷)迅速崛起,对全球经
- You should keep in mind ______ you should behave while trave
- .下列海洋表层等温线示意图中,表示南半球暖流的是:( )A B
- 八国联军发动侵华战争的直接目的是A.镇压中国人民的反帝斗争 B.攫取更多的侵略权益C.帮助清政府
- 已知直线l过坐标原点,抛物线C的顶点在原点,焦点在x轴正半轴上,若点A(-1,0)、B(0,8)关于l的对称点都在C上,
- 根据我国农业部2003年2月的《优势农产品区域布局规划》,四种农作物的优势生产区域如图所示。读下图回答图例①、②、③、④
- 某同学用两节干电池,一只电键、一只小灯泡和几根导线连成电路,发现闭合电键小灯不亮,断开电键小灯发光,以下分析正确的是(
- 根据《联合国宪章》,联合国成员国必须遵循的原则不包括 A.善意履行宪章义务 B.以集体武力解决国际争端 C.各会员国主权
- 关于氧化物Na2O2和Na2O,它们() A.阴阳离子个数比均为1:2 B.都含有非
- 如图所示,一根长为l的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹30°角且绷紧,小球A处于静止
- .如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G
- 小敏进行了认识唾液淀粉酶性质的实验,实验过程和结果如下表。试管编号 实验过程 1号 2号 3号 4号 ①注入物质 2ml
- 已知正四面体A—BCD,动点P在△ABC内,且点P到平面BCD的距离与点P到点A的距离相等,则动点P的轨迹为A.椭圆的一
- 将牛的胚胎分割后进行移植,可孕育出多头性状一致的小牛。下列哪项与该过程的实质是相同的 A.利用植物的根尖组织细胞培育大量
- 如图是某班在一次数学小测验中学生考试成绩分布图(满分100分),根据图中提供的信息回答问题:(1)该班共有多少学生? (
- 17.赤霉素具有促进植物茎秆伸长的作用,其作用机理如下图所示。遗传学研究表明,赤霉素对矮生玉米的作用效果明显,而对正常株
- 下列实验操作正确的是() A.连接仪器 B.塞进胶塞 C.倾倒液体
- 物质在应用中,只应用其化学性质的是 A.将活性炭放入冰箱中除去异味 B.用铅笔芯粉末使锁的开启变的
- 一段长为L,电阻为R的均匀电阻丝,把它拉制成3L长的均匀细丝后,切成等长的三段,然后把它们并联在一起,其电阻值为 []A



