初中 数学
欣赏图所示的团,并用两种方法分析图案的形成过程.

一个圆中有三个扇形甲、乙、丙,其中甲、乙所占总面积的百分比如图所示,那么扇形丙的圆心角是( )

A . 30º
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
如图,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个边或角的条件,你添加的条件是.

如图,  是边长为4的等边
是边长为4的等边  的中位线,动点P以每秒1个单位长度的速度,从点A出发,沿折线
的中位线,动点P以每秒1个单位长度的速度,从点A出发,沿折线  向点E运动;同时动点Q以相同的速度,从点B出发,沿
向点E运动;同时动点Q以相同的速度,从点B出发,沿  向点C运动,当点P到达终点时,点Q同时停止运动.设运动时间为
向点C运动,当点P到达终点时,点Q同时停止运动.设运动时间为  四点围成图形的面积S与时间t之间的函数图象是( )
四点围成图形的面积S与时间t之间的函数图象是( )
 是边长为4的等边
是边长为4的等边  的中位线,动点P以每秒1个单位长度的速度,从点A出发,沿折线
的中位线,动点P以每秒1个单位长度的速度,从点A出发,沿折线  向点E运动;同时动点Q以相同的速度,从点B出发,沿
向点E运动;同时动点Q以相同的速度,从点B出发,沿  向点C运动,当点P到达终点时,点Q同时停止运动.设运动时间为
向点C运动,当点P到达终点时,点Q同时停止运动.设运动时间为  四点围成图形的面积S与时间t之间的函数图象是( )
四点围成图形的面积S与时间t之间的函数图象是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某中学组织七年级同学到银川春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用60座客车,则多出1辆,且其余客车恰好坐满,已知45座客车日租金为每辆220元,60座客车日租金为每辆300元,试问:
-
(1) 七年级人数是多少?原计划租用45座客车多少辆?
-
(2) 要使每个同学都有座位,怎样租车更合算?
因式分解:a2b﹣ab+  b=.
b=.
 b=.
b=.
如图所示,四边形ABCD是平行四边形,E,F是对角线BD上的两点,∠1=∠2.

求证:
-
(1) BE=DF;
-
(2) AF//CE.
如图所示是函数  的部分图象,与x轴交于点
的部分图象,与x轴交于点  ,对称轴是直线
,对称轴是直线  .下列结论:
.下列结论:
(1) ;(2)
;(2)  ;(3)当
;(3)当  时,
时,  ;(4)
;(4)  ,(
,(  为任意实数).其中正确结论的个数有( )
为任意实数).其中正确结论的个数有( )
 的部分图象,与x轴交于点
的部分图象,与x轴交于点  ,对称轴是直线
,对称轴是直线  .下列结论:
.下列结论:(1)
 ;(2)
;(2)  ;(3)当
;(3)当  时,
时,  ;(4)
;(4)  ,(
,(  为任意实数).其中正确结论的个数有( )
为任意实数).其中正确结论的个数有( )

A . 1个
B . 2个
C . 3个
D . 4个
峨眉河是峨眉的一个风景点.如图,河的两岸  平行于
平行于  ,河岸
,河岸  上有一排间隔为
上有一排间隔为 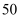 米的彩灯柱
米的彩灯柱  、
、  、
、  、…,小华在河岸
、…,小华在河岸  的
的  处测得
处测得  ,然后沿河岸走了
,然后沿河岸走了  米到达
米到达  处,测得
处,测得  ,求这条河的宽度(参考数据:
,求这条河的宽度(参考数据:  ,
,  ).
).
 平行于
平行于  ,河岸
,河岸  上有一排间隔为
上有一排间隔为 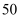 米的彩灯柱
米的彩灯柱  、
、  、
、  、…,小华在河岸
、…,小华在河岸  的
的  处测得
处测得  ,然后沿河岸走了
,然后沿河岸走了  米到达
米到达  处,测得
处,测得  ,求这条河的宽度(参考数据:
,求这条河的宽度(参考数据:  ,
,  ).
). 
如图,正方形网格中的  ,若小方格边长为1,请证明
,若小方格边长为1,请证明  为直角三角形,并求出其面积.
为直角三角形,并求出其面积.
 ,若小方格边长为1,请证明
,若小方格边长为1,请证明  为直角三角形,并求出其面积.
为直角三角形,并求出其面积. 
下列运算一定正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在边长为10的菱形  中,E是
中,E是  的中点,O是对角线的交点,矩形
的中点,O是对角线的交点,矩形  的一边在
的一边在  上,且
上,且  ,则
,则  的长为()
的长为()
 中,E是
中,E是  的中点,O是对角线的交点,矩形
的中点,O是对角线的交点,矩形  的一边在
的一边在  上,且
上,且  ,则
,则  的长为()
的长为() 
A . 5
B . 6
C .  D .
D . 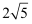
 D .
D . 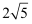
如图,  为
为  的直径,
的直径,  和过点
和过点  的切线互相垂直,垂足为
的切线互相垂直,垂足为  ,直线
,直线  、
、  交于点
交于点  ,
,  交
交  于点
于点  .
.
 为
为  的直径,
的直径,  和过点
和过点  的切线互相垂直,垂足为
的切线互相垂直,垂足为  ,直线
,直线  、
、  交于点
交于点  ,
,  交
交  于点
于点  .
. 
-
(1) 求证:
 平分
平分  ;
;
-
(2) 若
 ,
,  ,求
,求  的长.
的长.
如图,一次函数  与反比例函数
与反比例函数  的图象交于
的图象交于  两点,当
两点,当  时
时  的取值范围是.
的取值范围是.
 与反比例函数
与反比例函数  的图象交于
的图象交于  两点,当
两点,当  时
时  的取值范围是.
的取值范围是. 
若某正数的平方根是a+3和2a-15,则a的值是 ( )
A . 4
B . -1
C . 1
D . 2
计算:  ×
×  +|
+|  ﹣3|.
﹣3|.
 ×
×  +|
+|  ﹣3|.
﹣3|.
如图,在等腰三角形  中,
中,  ,
, 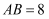 ,
,  为底边
为底边  上一动点(不与点
上一动点(不与点  重合),
重合),  ,
,  ,垂足分别为
,垂足分别为  ,则
,则  .
.
 中,
中,  ,
, 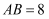 ,
,  为底边
为底边  上一动点(不与点
上一动点(不与点  重合),
重合),  ,
,  ,垂足分别为
,垂足分别为  ,则
,则  .
. 
如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )

A . 1﹣  π
B .
π
B .  ﹣
﹣  C . 2﹣
C . 2﹣  D . 2﹣
D . 2﹣  π
π
 π
B .
π
B .  ﹣
﹣  C . 2﹣
C . 2﹣  D . 2﹣
D . 2﹣  π
π
如图,BE是∆ABC的角平分线,点D是AB边上一点,且∠DEB=∠DBE

-
(1) DE与BC平行吗?为什么?
-
(2) 若∠A=40°,∠ADE=60°,求∠C的度数.
计算![]() 所得的结果是( )
所得的结果是( )
A.8 B.![]() C.16 D.
C.16 D.![]()
最近更新
- My friend showed me round the town, ______ was very kind of
- 备受瞩目的民营银行试点,近日终于掀起了“红盖头”。2014年3月, 银监会披露,包括阿里巴巴和腾讯在内的十家公司将参与民
- 下图是某植物叶肉细胞中光合作用和呼吸作用的物质变化示意简图,其中a、b表示物质,①~④表示生理过程。据图回答:(1)图中
- (本小题15分) 生产某种产品吨时,所需费用是元,当出售这种产品吨时,每吨价格是(是常数)元,如果生产出来的这种产品能全
- 某学生用锌片、铜片、发光二极管、滤纸、导线等在玻璃片制成如图所示的原电池,当滤纸用醋酸溶液润湿时,二极管发光.下列有关该
- 伏尔泰、孟德斯鸠和卢梭是启蒙运动时期的主要代表人物,这三位思想家被称为法兰西的“自由三剑客”。主要是因为他们()①抨击天
- We mustsend the poor man to hospital because he was
- 下列各句中加点的成语使用正确的一句是( ) A.在这次举行的当代书法展上,各种书体与风格的作品等量齐观,保证了展览的
- He _____ his grandmother if he is free. A. will visit
- 设点P是双曲线-=1上一点,F1、F2为它的焦点,如果∠PF1F2=75°,∠PF2F1=15°,则双曲线的离心率是__
- 下列植物食用部分属于茎的一项是 A.番薯 B.洋葱 C.莲藕 D.西红柿
- 2014年1月以来,乌克兰局势持续动荡,3月,该国南部黑海沿岸的克里米亚自治区要求“并入”俄罗斯。据此回答1~3题。 1
- 发生在三国两晋南北朝时以少胜多的战役是( )A.巨鹿之战 B.官渡之战 C.赤壁之战 D.淝
- 完成下列单位换算:3 t=_____kg72 km/h=_____ m/s40 cm/s2=_____m/s22 N/g
- 我国政府的职能决定政府的性质。
- (宋太祖)因谓(赵)普曰:“五代方镇残虐,民受其祸,朕今选儒臣干事者百余,分治大藩,纵皆贪,亦未及武臣一人也。”宋太祖据
- The year was 1932. AmeliaEarhart was flying alone from North
- 背景:今年的央视“3.15”晚会,在全国人民面前揭穿了欧典地板“德国制造”的谎言:“德国总部”根本不存在。几天后,欧典企
- 图16为世界某年某月的等压线分布图(单位:百帕)。图中甲地是一片缓和起伏的大草原。读图,回答下列问题。 (1)
- 下图为一组剖面示意图,反映了我国华北某地区土地利用状况由图1时期至图4时期的历史变化过程(图1时期至图4时期气候变化甚微



