初中 数学
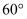 , 则这个时刻是( )
, 则这个时刻是( )
 的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的
的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的  )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn , 则P2018﹣P2017的值为( )
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn , 则P2018﹣P2017的值为( ) 
 B .
B .  C .
C .  D .
D . 
-
(1) 3x2﹣7x=0
-
(2) (x﹣2)(2x﹣3)=2(x﹣2)

 B .
B .  C .
C .  D .
D . 
 的是( )
的是( )
 B .
B . 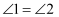 C .
C .  D .
D . 
 是关于x的一元二次方程,则m的取值范围是.
是关于x的一元二次方程,则m的取值范围是.
 分解成两个一次方程,正确的是( )
分解成两个一次方程,正确的是( )
 B .
B .  C .
C .  D .
D . 

 ,
,  的二元一次方程组
的二元一次方程组  ,甲解对了,得
,甲解对了,得  ;乙写错了
;乙写错了  ,得
,得  ,试求方程组中
,试求方程组中  ,
,  ,
,  的值.
的值.
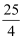 ,那么这个数为.
,那么这个数为.年龄/岁 | 12 | 13 | 14 | 15 |
人数 | 5 | 15 | x | 12﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )

-
(1) 如图1,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:DE=DF;
-
(2) 如图2,点E,点F分别在AB,AC上,且∠EDF=2∠B.求证:DE=DF.

问题:如图1,在正方形ABCD内有一点P,PA=![]() ,PB=
,PB=![]() ,PC=1,求∠BPC的角度.
,PC=1,求∠BPC的角度.
分析:根据已知条件比较分散的特点,我们可以通过旋转变换,将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转900,得到了△BP1A(如图2),然后连接PP1.
 |
解决问题:请你通过计算求出图2中∠BPC的角度.
类比研究:如图3,若在正六边形ABCDEF内有一点P,且PA=![]() ,PB=4,PC=2.
,PB=4,PC=2.
(1)请你通过计算求出∠BPC的度数.
(2)直接写出正六边形ABCDEF的边长为 .
四个实数 0 , 
A . 0 B . C .
D .
方程组![]() 的解是
的解是
在矩形ABCD中,边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处(如图1).


图1 图2
(1)如图2,设折痕与边BC交于点O,连接,OP、OA.已知△OCP与△PDA的面积比为1:4,求边AB的长;
(2)动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN、 PA,交于点F,过点M作ME⊥BP于点E.
①在图1中画出图形;
②在△OCP与△PDA的面积比为1:4不变的情况下,试问动点M、N在移动的过程中,线段EF的长度是否发生变化?请你说明理由.
- 已知向量a=(x+z,3),b=(2,y-z),且a⊥b,若x,y满足不等式|x|+|y|≤1,则z的取值范围为().
- 两千多年前,孔子提出了“君子和而不同”的思想。这一思想对中华文化产生了深远影响。“和而不同”反映了中华文化具有的特点是
- 今天的民众获得自由表达意见、畅所欲言、不受严密控制的观念的权力,主要得益于( ) A.罗马法系 B.
- 2017年11月1日,中国环境网报道,近日,从中科院大连化物所获悉,该所催化基础国家重点实验室王集杰博士、李灿院士等人
- 阅读下面的材料,根据要求写一篇不少于800字的文章。(60分)生活如镜,“时时勤拂拭,莫使惹尘埃。”花鸟、天气、万物皆因
- (4分)物体以5m/s的初速度沿光滑斜槽向上做直线运动,经4 s滑回原处时速度大小仍为 5 m/s,则物体的速度变化为
- 北半球夏至日到秋分日,下列现象正确的是( ) A.北极圈及其以北的极昼范围逐渐扩大B.南极圈及其以南地区的极夜范围
- V mL Al2(SO4)3溶液中含有Al3+m g,取 mL该溶液用水稀释至4V mL,则SO物质的量浓度为 () A
- (本题共16分) 已知:碱金属或碱土金属(Ⅱ族)与H2在隔绝空气加热时要以发生反应,生成离子型金属氢化物,如NaH、Ca
- 下列叙述错误的是:A.远视眼是由于晶状体太薄或眼球距离过短造成的;B.远处射来的光经过近视眼的水晶体折射,只能在视网膜后
- 在高200米的山顶上,测得山下一塔顶与塔底的俯角分别为30o、60o,则塔高为( ) A.米 B.
- 若对满足条件x+y+3=xy (x>0,y>0)的任意x、y,(x+y)2-a(x+y)+1≥0恒成立,则实数a的取值范
- 设 , 若有且仅有三个解,则实数的取值范围是( )A. B. C
- 下列各句中,加点的成语使用恰当的一句是() A.今年春节期间,镇里举行了一场别无二致的茶话会,向返乡过节的流动党员们通报
- 日本明蟹壳色有三种情况:灰白色、青色和花斑色。其生化反应原理如右图所示。基因A控制合成酶1,基因B控制合成酶2,基因b控
- 有关我国交通与与城市区位的叙述,不正确的是( ) A.古代南方城市沿河设城是一般规律 B.古代北方城市大都位于大
- The captain told the sailors to their sprits when they were
- 人体神经细胞与肝细胞的形态结构和功能不同,其根本原因是这两种细胞的 A.细胞核中DNA的碱基排列顺序不同
- (9分)某研究性学习小组欲利用下列装置进行相关气体制取的探究,请你分析并填空。 (1)写出图中仪器a、b的名称 a
- 关于作用力和反作用力,下列说法正确的是…( )A.地球对重物的作用力大于重物对地球的作用力B.当作用力是摩擦力时,



